https://youtu.be/Y0lT9Fck7qI?si=qZtxOINcvanqqhvu
최종 코드
class Solution:
def climbStairs(self, n: int) -> int:
# n 이 되기 위해, 1,2 로 구성된게 몇개??
# dfs
# 트리..
# DP
# cache + memorization
# DP- bottom up
"""
dp[1] = 1
dp[2] = dp[1] + 1
dp[3] = dp[1] + dp[2]
dp[4] = dp[3] + dp[2]
dp[5] = dp[4] + dp[3]
"""
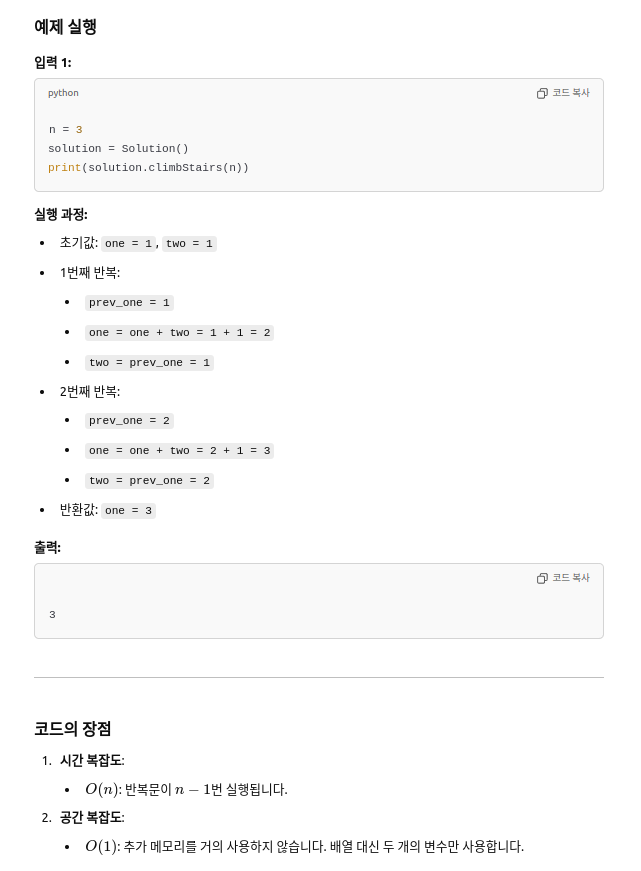
one, two = 1, 1
for i in range(n-1):
prev_one = one # 현재 `one` 값(dp[i-1])을 임시로 저장
one = one + two # 점화식: dp[i] = dp[i-1] + dp[i-2], 현재 계단까지의 방법 수
two = prev_one # `two`를 이전 `one` 값(dp[i-1])으로 갱신, 즉 dp[i-2] = dp[i-1]
return one

class Solution:
def climbStairs(self, n: int) -> int:
one, two = 1, 1
for i in range(n-1):
temp = one
one = one + two
two = one
return one
Time & Space Complexity
- Time complexity: O(n)
- Space complexity: O(1)
"Climbing Stairs" 문제를 해결하는 데 있어 최적화된 방식으로 작성되었습니다.
이 접근법은 **Dynamic Programming (DP)**를 활용하지만,
추가적인 공간을 절약하기 위해 배열을 사용하지 않고 두 개의 변수(one과 two)만 사용하는 Bottom-Up 방식입니다.

https://youtu.be/VTjekgLvsuA?si=i5Ri1Q7Qs7X4qdXM
해결 함
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 2:
return n
else:
dp = [0] * (n+1)
dp[1] = 1 # only 1 사용
dp[2] = dp[1] + 1 # 1사용, 2사용 = 2
for i in range(3, n+1):
dp[i] = dp[i-1] + dp[i-2] # 이전 스텝에서 1칸, 이전전에서 2칸
return dp[n]
class Solution:
def climbStairs(self, n: int) -> int:
dp = {}
dp[1] = 1
dp[2] = dp[1]+1
dp[3] = dp[2] + dp[1]
if n<4:
return dp[n]
for i in range(4, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
최종 코드
class Solution:
def climbStairs(self, n: int) -> int:
one, two = 1, 1
for i in range(n-1):
tmp = one
one = one + two
two = tmp
return one
내 코드
class Solution:
def climbStairs(self, n: int) -> int:
if n==1:
return 1
elif n==2:
return 2
else: # n>2:
dp = [0] * (n+1)
dp[1] =1
dp[2] = 1 + dp[1]
for i in range(3, n+1):
dp[i] = dp[i-1]+dp[i-2]
return dp[n]'job 인터뷰 > 코테(Matroid) 준비' 카테고리의 다른 글
| Tree: 543. Diameter of Binary Tree ★ (0) | 2025.01.16 |
|---|---|
| BST: 701. Insert into a Binary Search Tree (0) | 2025.01.15 |
| [위상정렬] Graphs(싸이클탐지): 207. Course Schedule (2) | 2024.12.16 |
| Tree: 98. Validate Binary Search Tree (0) | 2024.12.15 |
| 173. Binary Search Tree Iterator (0) | 2024.12.14 |