문제 LeetCode 745. Prefix and Suffix Search를 해결하는 Trie 기반 풀이를 제공해드릴게요.
접두사(prefix)와 접미사(suffix)를 동시에 만족하는 단어를 빠르게 찾기 위해, 특수한 방식으로 Trie를 구성합니다.
✅ 핵심 아이디어:
모든 단어에 대해 "suffix#prefix" 형태로 key를 만들어서 Trie에 저장합니다.
예시
- 단어 "apple" → "e#apple", "le#apple", ..., "#apple" 등으로 여러 key 생성
- 검색할 때 "suff#pref" 형식으로 Trie에서 찾기
✅ 완성된 코드 (딕셔너리 기반 Trie 사용)
class TrieNode:
def __init__(self):
self.children = {} # 문자 → 자식 노드
self.weight = -1 # 현재 경로에서의 가장 큰 인덱스
class WordFilter:
def __init__(self, words: List[str]):
self.root = TrieNode()
for weight, word in enumerate(words):
word_with_sep = word + "#" + word
# 모든 접미사에 대해 접미사#단어 구조 만들기
for i in range(len(word) + 1):
key = word[i:] + "#" + word
self._insert(key, weight)
def _insert(self, key: str, weight: int):
node = self.root
for ch in key:
if ch not in node.children:
node.children[ch] = TrieNode()
node = node.children[ch]
node.weight = weight # 경로마다 가장 큰 인덱스 저장
def f(self, pref: str, suff: str) -> int:
node = self.root
search_key = suff + "#" + pref # 검색 키 구성
for ch in search_key:
if ch not in node.children:
return -1
node = node.children[ch]
return node.weight
✅ 예시 사용법
wf = WordFilter(["apple"])
print(wf.f("a", "e")) # ➜ 0 (apple)
print(wf.f("ap", "le")) # ➜ 0 (apple)
print(wf.f("b", "e")) # ➜ -1 (해당 단어 없음)✅ 시간 복잡도
- 초기화: O(N * L²)
(N = 단어 수, L = 단어 길이, 접미사 × 단어) - 검색: O(L) (prefix + suffix 길이)
✅ 왜 이 방식이 좋은가요?
| 특징 | 설명 |
| Trie 사용 | 접두사 + 접미사 조합을 빠르게 탐색 가능 |
| # 문자 | 접두사/접미사 구분용 (알파벳보다 큰 ASCII 문자) |
| 경로마다 weight 저장 | 중복된 prefix/suffix 조합이 있어도 가장 큰 인덱스 유지 가능 |



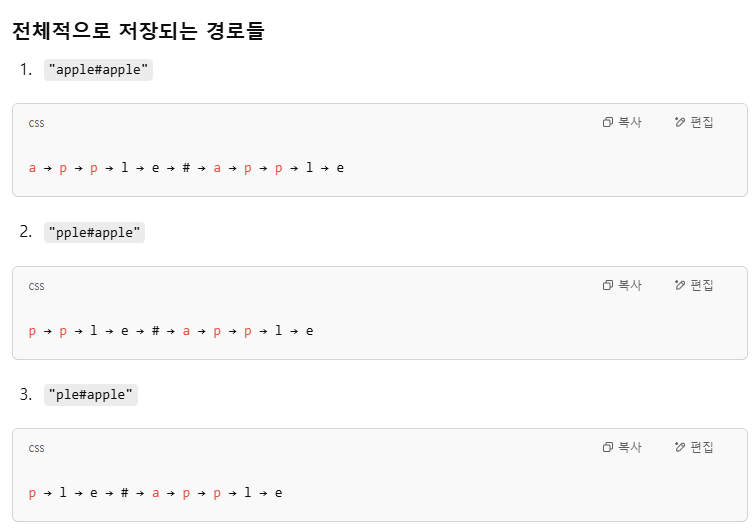
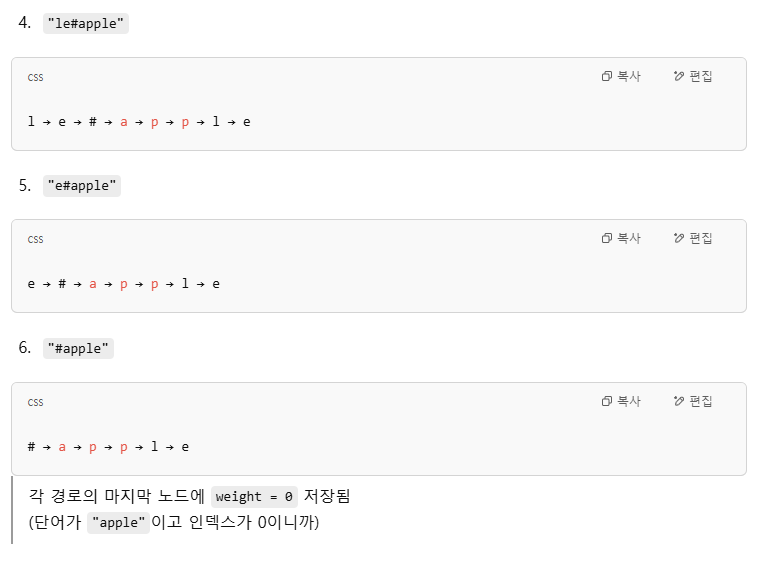

왜 "prefix#suffix"가 아니라 "suffix#prefix" 형식으로 저장하는지를 직관적으로 설명
✅ 핵심 목표:
우리는 주어진 prefix와 suffix를 동시에 만족하는 단어를 빠르게 찾아야 해요.
즉,
❓직관적인 질문
"그럼 prefix#suffix 로 Trie에 저장하고, 나중에 pre#fix로 검색하면 되는 거 아닌가요?"
→ 언뜻 보면 그렇게 해도 될 것처럼 보이죠.
하지만 Trie의 특성상 "앞에서부터 한 글자씩 내려가며 찾는" 구조이기 때문에,
prefix가 앞에 오면 "접두사만" 빠르게 찾는 구조가 돼버립니다.
⚠️ 문제점: "prefix#suffix" 방식의 Trie는 접미사 처리에 약함
예: "apple" 저장
"ap#le" 형태로 저장했다고 해봅시다.
Trie에서 "a → p → # → l → e" 라고 따라가야 하는데,
나중에 접미사가 달라진다면 → "a → p → # → x → x" 는 안 따라가짐.
즉, 접두사는 빠르게 찾을 수 있지만
접미사가 바뀌면, 그 뒤 경로를 Trie가 따라가기 힘듦
→ Trie 구조의 효율성이 깨짐!
✅ 반대로 "suffix#prefix"는 접두사/접미사 둘 다 검색 가능
예: "apple"을 "le#ap"로 저장
- 검색할 때 f("ap", "le") → "le#ap"
- Trie는 "l → e → # → a → p" 경로를 따라가며 찾음
- 접미사 "le" 기준으로 먼저 좁히고,
이어서 접두사 "ap"를 확인하는 구조
→ 훨씬 효율적인 분기 구조가 됨!
💡 Trie의 본질을 다시 생각해보면:
Trie는 "앞에서부터 한 글자씩" 따라가며 문자열을 탐색하는 구조예요.
→ 그러니까 우리가 Trie에 넣는 키(key)는
**"검색할 때 앞에서부터 알고 있는 정보"**가 먼저 와야 해요.
✅ 요약 비교
| 방식 | 설명 | 문제점 |
| prefix#suffix | 접두사를 기준으로 트리를 탐색 | 접미사 검색이 어려움 (Trie는 뒤를 잘 못 봄) |
| suffix#prefix | 접미사를 기준으로 먼저 좁히고, 접두사 확인 | ✅ 효율적, 접미사와 접두사 둘 다 검색 가능 |
🎯 결론
우리가 접미사 + 접두사 순서로 suffix#prefix를 만드는 이유는,
Trie의 탐색 방식이 "앞에서부터 한 글자씩" 이기 때문이에요.
접미사를 앞에 두면, 접미사별로 먼저 Trie에서 분기를 나누고,
그 뒤에 접두사 정보를 붙이면 둘 다 효율적으로 검사 가능해요!
Hashmap 사용
class WordFilter:
def __init__(self, words: List[str]):
self.mp = {} # 접두사 + '$' + 접미사를 key로, 인덱스를 value로 저장할 딕셔너리
for i, w in enumerate(words): # 단어 리스트를 하나씩 순회하며 (단어, 인덱스)
for j in range(len(w)): # 접두사를 만들기 위한 반복 (앞에서 j+1 글자까지 자름)
pref = w[:j + 1] # 접두사: 단어의 앞에서부터 j+1 글자까지
for k in range(len(w)): # 접미사를 만들기 위한 반복 (뒤에서 k부터 끝까지 자름)
# "접두사$접미사" 형태로 key를 만들고, 현재 단어의 인덱스를 저장
# 같은 key가 여러 번 나올 경우, 가장 마지막(가장 큰 인덱스)으로 덮어쓰기
cur = pref + "$" + w[k:]
self.mp[cur] = i # 해당 조합에 대해 가장 최근 인덱스를 저장
def f(self, pref: str, suff: str) -> int:
# 검색할 때도 "접두사$접미사" 형태의 key를 만들어 딕셔너리에서 찾음
s = pref + "$" + suff
# key가 존재하지 않으면 -1 반환 (조건에 맞는 단어가 없음)
if s not in self.mp:
return -1
# 존재하면 저장된 인덱스를 반환 (가장 마지막에 등장한 단어)
return self.mp[s]
✅ 핵심 아이디어 요약
- 이 구현은 Trie를 사용하지 않고, dict를 사용하여
"prefix + '$' + suffix" 조합을 모든 가능한 경우에 대해 미리 저장합니다. - $는 접두사와 접미사를 구분하는 구분자 문자로 사용되며,
실제 단어에 포함되지 않기 때문에 충돌이 없습니다. - O(N * L²) 만큼 미리 조합을 만들어두고,
f() 함수 호출 시 O(1)로 검색이 가능합니다.
✅ 예시
단어: "apple", 인덱스: 0
→ 생성되는 key 예시:
| prefix | suffix | key (pref$suff) |
| a | apple | a$apple |
| a | pple | a$pple |
| ap | ple | ap$ple |
| app | le | app$le |
| appl | e | appl$e |
| apple | e | apple$e |
...
필요하시면 이 방식과 Trie 방식의 속도/메모리 차이도 비교해드릴게요!
또는 이 방식으로 접두사/접미사 검색이 어떻게 빠르게 되는지도 시각적으로 도와드릴 수 있어요 😊
나의 말:
ChatGPT의 말:
좋은 질문이에요!
이제 Dict 방식과 Trie 방식을 비교해서
속도/메모리/유연성 등 성능 측면에서 어떤 차이가 있는지 표로 명확히 정리해드릴게요.
✅ 비교 대상
| 방식 | 설명 |
| Dict 방식 | "prefix$suffix"를 key로 딕셔너리에 저장 |
| Trie 방식 | "suffix#prefix" 형태로 문자를 한 글자씩 Trie 노드에 저장 |
✅ 성능 비교표
| 항목 | Dict 방식 | Trie 방식 |
| 🔄 초기화 시간 | O(N × L²) | O(N × L²) |
| 🔍 검색 시간 | O(1) (딕셔너리 lookup) | O(L) (Trie에서 문자 하나씩 탐색) |
| 🧠 메모리 사용 | 많음 (문자열 전체를 key로 저장) | 덜 많음 (문자를 경로로 공유) |
| 📦 저장 구조 | "prefix$suffix" → 인덱스 (중복 key 존재) | 경로마다 문자 노드로 구성, 경로 공유 |
| 🧩 유연성 | 구현이 간단하고 직관적 | 조금 복잡하지만 더 압축적 |
| ⏱ 실제 속도 | 빠름 (작은 입력에선 매우 우수) | 길거나 중복 많은 단어에 더 효율적 |
| 🔁 중복 제거 | key로 자동 덮어씀 | Trie 경로 재사용으로 중복 최소화 |
✅ 간단 정리
| 상황추천 | 방식 | 이유 |
| 단어 수 적고 구현 간단하게 하고 싶을 때 | Dict 방식 | 코드가 짧고 검색 속도 빠름 |
| 메모리 아끼고 구조화된 데이터 다룰 때 | Trie 방식 | 경로 공유, 확장성 좋음 |
| 접두사/접미사 조합 수 많을 때 | Trie 방식 | 중복 최소화, 메모리 절약 가능 |
✅ 결론
| 핵심 기준 | Dict 방식 | Trie 방식 |
| 속도 | 매우 빠름 (O(1) 검색) | 조금 느림 (O(L) 검색) |
| 메모리 | 더 많이 사용 | 더 적게 사용 |
| 복잡도 | 구현 쉬움 | 구조화된 설계 필요 |
| 추천 | 단어 수 적고 단순한 문제 | 접두사/접미사 검색이 많은 대형 문제 |
'LeetCode > NeetCode' 카테고리의 다른 글
| [Trees: Segment Tree] 307. Range Sum Query - Mutable (0) | 2025.04.08 |
|---|---|
| [Trees: Union Find] 721. Accounts Merge ★★★★★★★★ (0) | 2025.04.07 |
| [Linked Lists: Fast and Slow Pointers] 876. Middle of the Linked List (0) | 2025.04.06 |
| [Prefix Sums] 724. Find Pivot Index (0) | 2025.04.05 |
| [Prefix Sums] 304. Range Sum Query 2D - Immutable (적분영상) (0) | 2025.04.05 |