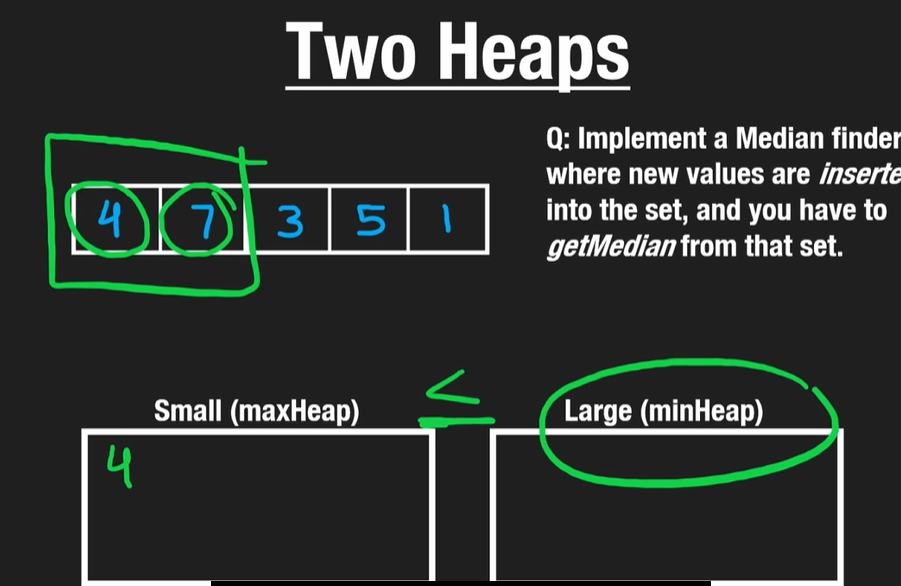
중간값(median)을 빨리 구하기 위해서
2개의 heap 을 만들고
small heap 은 max heap 으로, large heap 은 min heap 으로 만들면
small heap 의 최대값과 large heap 의 최소값을 비교해서,
median 값을 빨리 계산할 수 있음
그런데, 두개 heap 의 사이즈 차이가 2 이상(같거나 1개 정도는 그냥 둠) 나면 , heap 조절해줘야 함
small heap 크기 > large heap 크기 +1 이면, small heap 의 최대값을 large heap 으로 보내고
small heap 크기 +1 < large heap 크기 이면, large heap 의 최소값을 small heap 으로 보
이 코드는 데이터 스트림에서 중간값(Median)을 실시간으로 추적하는 클래스를
heapq (Python의 우선순위 큐)를 이용해 구현한 것입니다.
import heapq # 파이썬 내장 최소 힙 모듈 (최대 힙은 지원 안 함, 부호 반전으로 구현)
class Median:
def __init__(self):
# small: 최대 힙 역할 (중간값보다 작은 값들 저장) → 부호를 반대로 넣어 최소 힙을 최대 힙처럼 사용
# large: 최소 힙 역할 (중간값보다 큰 값들 저장)
self.small, self.large = [], []
def insert(self, num):
# 새로운 숫자를 최대 힙(small)에 먼저 넣음 (heapq는 최소 힙이므로 부호 반대로)
heapq.heappush(self.small, -1 * num)
# 두 힙의 정렬 순서가 깨지는 경우 처리
# 최대 힙의 최댓값(-self.small[0])이 최소 힙의 최솟값(self.large[0])보다 크면
# 순서가 역전된 것이므로 값을 하나 옮겨서 균형 맞춤
if (self.small and self.large and (-1 * self.small[0]) > self.large[0]):
val = -1 * heapq.heappop(self.small) # 최대 힙에서 가장 큰 값 꺼냄 (음수 -> 양수로 복원)
heapq.heappush(self.large, val) # 그 값을 최소 힙에 삽입
# 두 힙의 크기 차이가 2 이상 나지 않도록 균형 맞추기
# small이 더 많을 경우 → 하나를 large로 이동
if len(self.small) > len(self.large) + 1:
val = -1 * heapq.heappop(self.small) # 다시 양수로 복원 후
heapq.heappush(self.large, val) # large에 넣음
# large가 더 많을 경우 → 하나를 small로 이동
if len(self.large) > len(self.small) + 1:
val = heapq.heappop(self.large) # 그대로 꺼냄
heapq.heappush(self.small, -1 * val) # 부호를 바꿔 small에 삽입 (최대 힙 형태 유지)
def getMedian(self):
# small(최대 힙)이 더 크면, 중간값은 small의 루트값 (-self.small[0])
if len(self.small) > len(self.large):
return -1 * self.small[0]
# large(최소 힙)가 더 크면, 중간값은 large의 루트값 (self.large[0])
elif len(self.large) > len(self.small):
return self.large[0]
# 두 힙의 크기가 같으면 → 중간에 있는 두 값의 평균 반환
return (-1 * self.small[0] + self.large[0]) / 2'Coding Test > 알고리즘 이론' 카테고리의 다른 글
| Combinations 조합 (0) | 2025.04.09 |
|---|---|
| Subsets 부분집합 (0) | 2025.04.09 |
| Iterative DFS (반복형 깊이 우선 탐색) (0) | 2025.04.08 |
| 세그먼트 트리 Segment Tree (0) | 2025.04.08 |
| Trees: Union-Find (Disjoint Set Union, DSU) (0) | 2025.04.07 |