https://youtu.be/tWVWeAqZ0WU?si=zOJL3C3EY4LII59T
1. Graph 에 대한 DFS (깊이 탐색) 과 BFS (너비 탐색)

graph = {
'a': ['c', 'b'],
'b': ['d'],
'c': ['e'],
'd': ['f'],
'e': [],
'f': [],
}# Online Python - IDE, Editor, Compiler, Interpreter
graph = {
'a': ['c', 'b'],
'b': ['d'],
'c': ['e'],
'd': ['f'],
'e': [],
'f': [],
}
def depthFirstSearchPrint(graph, source):
stack = [source]
while(len(stack) >0):
cur = stack.pop()
print(cur)
for neighbor in graph[cur]:
stack.append(neighbor)
def depthFirstSearchRecursionPrint(graph, source):
print(source)
for neighbor in graph[source]:
depthFirstSearchRecursionPrint(graph, neighbor)
from collections import deque
def breadthFirstSearchPrint(graph, source):
q = deque([source])
while(len(q) >0):
cur = q.popleft()
print(cur)
for neighbor in graph[cur]:
q.append(neighbor)
print('depthFirstSearchPrint')
depthFirstSearchPrint(graph, 'a')
"""
출력 : abdfce
a 이후, c, b 순서대로 stack 에 쌓이는데, stack 이므로,
나중에 쌓이는게 먼저 나오다보니, b, c 순서대로 나오게되서,
abdfce 이렇게 출력이 됨
"""
print('depthFirstSearchRecursionPrint')
depthFirstSearchRecursionPrint(graph, 'a')
"""
출력 : acebdf
재귀를 사용하므로,
a 이후, c, b 순서대로 함수를 call 하므로, c, b 순서대로 나오게되서,
acebdf 이렇게 출력이 됨
"""
print('breadthFirstSearchPrint')
breadthFirstSearchPrint(graph, 'a')
"""
출력 : acbedf
큐를 사용하므로, 먼저 들어간게 먼저 나옴.
그래서, 레벨별로 출력된다고 보면 됨.
acebdf 이렇게 출력이 됨
"""
2. Graph 에 대한 인접 리스트
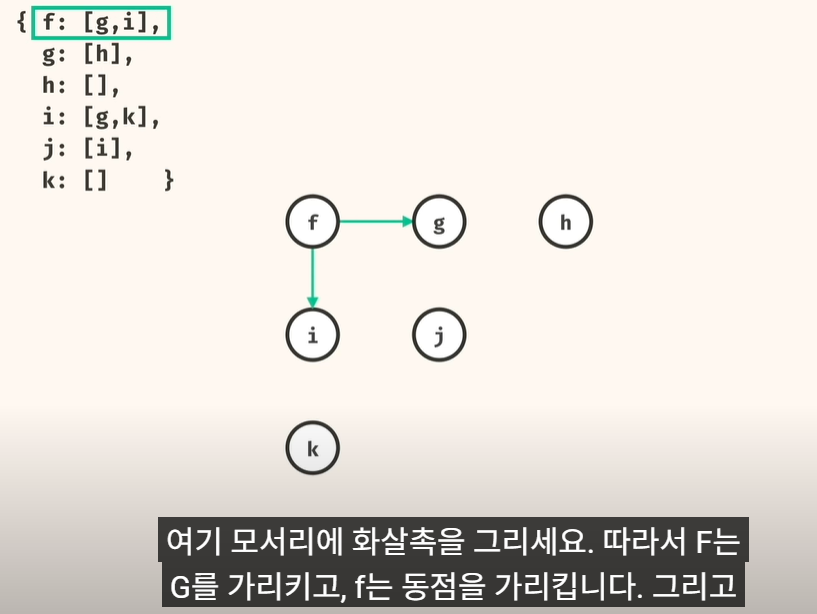
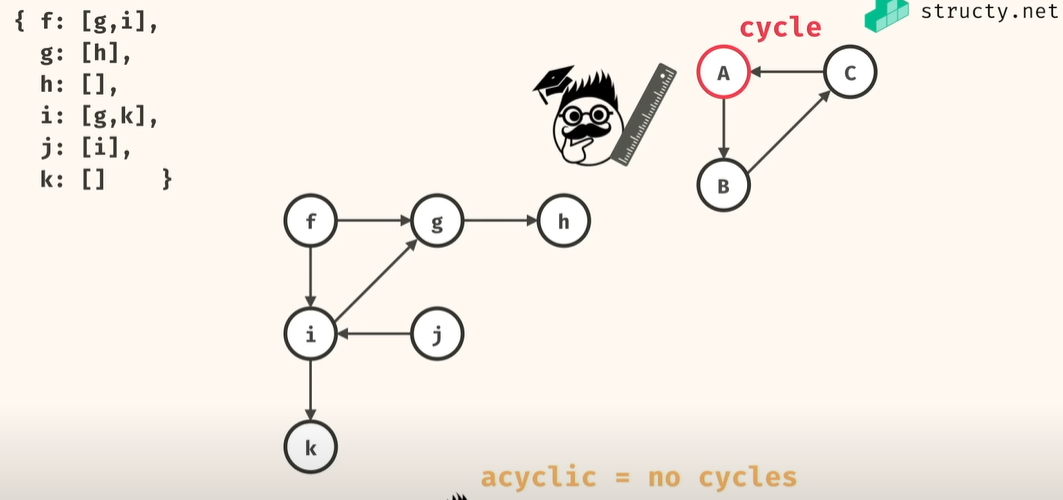
문제 유형1) 그래프가 주어졌을때, src 에서 dst 로 가는 경우 갈수 있는지? 없는지?
=> dfs 나 bfs 로 풀수 있다.

시간 공간 복잡도 면에서..
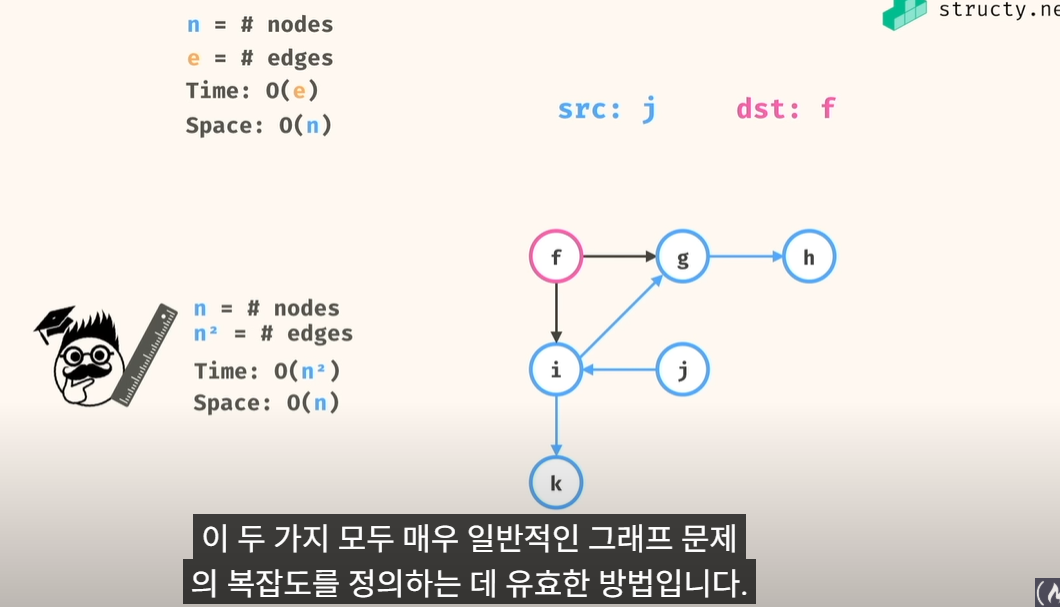
에지 개수가 n^2 되는 경우는 양방향 일때. => 시간 복잡도는 O(n^2), 공간복잡도는 O(n)
문제 유형1) 경로 찾기 문제: DFS 재귀 방법 솔루션
# Online Python - IDE, Editor, Compiler, Interpreter
graph = {
'a': ['b', 'c'],
'b': ['d'],
'c': [],
'd': ['e'],
'e': []
}
def hasPathDFSRecursion(graph, src, dst):
if src == dst:
return True
for neighbor in graph[src]:
if hasPathDFSRecursion(graph, neighbor, dst):
# if True 이면 재귀를 call 한 부모에. return true 하면되고
# False 이면, 다음 검색을 하면됨
return True
# 여기까지 왔는데, True 가 반환 안됬으면, 못찾은 것임
return False
# True인 경우
print(hasPathDFSRecursion(graph, 'a', 'e')) # 👉 a → b → d → e 경로 존재 → True
# False인 경우
print(hasPathDFSRecursion(graph, 'c', 'e')) # 👉 c는 아무 곳에도 연결 안 됨 → False
문제 유형1) 경로 찾기 문제: BFS 방법 솔루션
# Online Python - IDE, Editor, Compiler, Interpreter
graph = {
'a': ['b', 'c'],
'b': ['d'],
'c': [],
'd': ['e'],
'e': []
}
from collections import deque
def hasPathBFS(graph, src, dst):
q = deque([src])
while len(q) > 0:
cur = q.popleft()
if cur == dst:
return True
for neighbor in graph[cur]:
q.append(neighbor)
return False
# True인 경우
print(hasPathBFS(graph, 'a', 'e')) # 👉 a → b → d → e 경로 존재 → True
# False인 경우
print(hasPathBFS(graph, 'c', 'e')) # 👉 c는 아무 곳에도 연결 안 됨 → False
문제 유형2) 그래프가 주어졌을때, undirected path (양방향 경로) 문제
에지 정보를 줌
[i, j] => 의미: i 와 j 사이에 연결이 있다는 의미이고, 방향이 없기때문에, i->j, j->i 둘다 이동 가능

그래서 이 'edges 리스트' 를 'adjacency 인접 리스트' 로 '변환'해야 함


def buildGraph(edges):
graph = {}
for s, d in edges:
if s not in graph:
graph[s] = []
if d not in graph:
graph[d] = []
graph[s].append(d)
graph[d].append(s)
return graph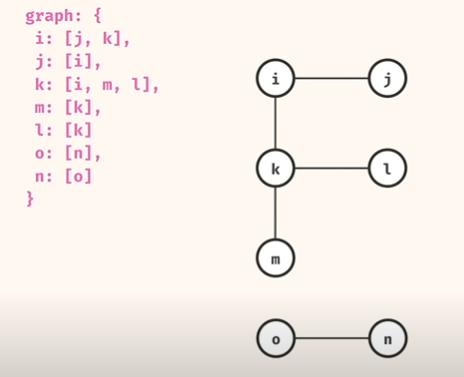
j-k 간선을 추가 함으로써, Cycle 이 생김!!
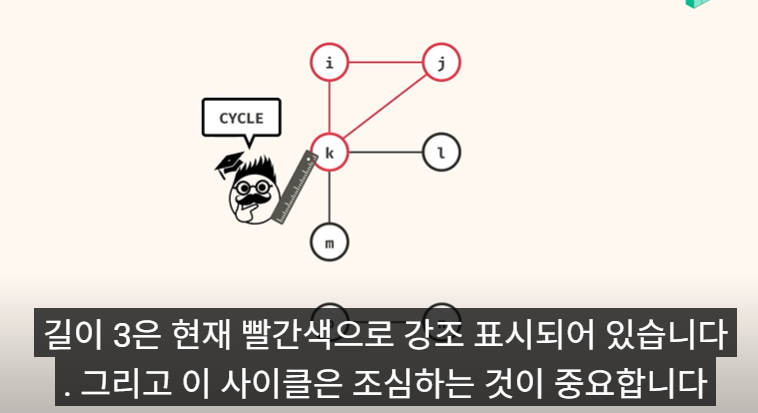
그리고, o-n 도 원래 Cycle 이 었음.
Cycle 이 있는 부분은 특수한 처리를 하지않으면, 무한 loop 에 빠지므로, 로직 구현할때.. 주의 필요!
※ undirected edge 문제는 섬이 몇개냐?? 이런 류의 문제들이 있음
※ undirected edge 에서 경로 가능한지?
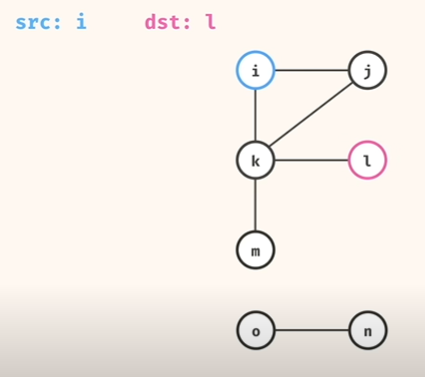
'Cycle' 에 빠지지 않기 위해, 'set()' 을 이용한 '방문처리 visit' 필요!

그러나, 아래처럼, src 와 dst 가 같은 섬에 있지 않는 경우에는, dfs, bfs 로 찾는 것은.. 최악의 경우.. 엄청 시간이 많이 걸림

https://structy.net/problems/undirected-path
Structy - Learn data structures and algorithms, efficiently.
Structy is the best platform for learning data structures and algorithms. Learn all the topics required for technical interviews through a strong sense of progression with Structy.
structy.net
def buildGraph(edges):
graph = {}
for s, d in edges:
if s not in graph:
graph[s] = []
if d not in graph:
graph[d] = []
graph[s].append(d)
graph[d].append(s)
return graph
def undirectedPath(edges, nodeA, nodeB):
graph = buildGraph(edges)
print(graph)
return hasPath(graph, nodeA, nodeB)
def hasPath(graph, src, dst):
if src == dst:
return True
for neighbor in graph[src]:
if hasPath(graph, neighbor, dst): # True
return True
return False
edges = [
['i', 'j'],
['k', 'i'],
['m', 'k'],
['k', 'l'],
['o', 'n']
]
print(undirectedPath(edges, 'm', 'j')) # -> true
print(undirectedPath(edges, 'k', 'o')) # -> false
이 코드는, cycle 이 고려되지 않았기 때문에,
RecursionError: maximum recursion depth exceeded in comparison 에러 발생!
{'i': ['j', 'k'], 'j': ['i'], 'k': ['i', 'm', 'l'], 'm': ['k'], 'l': ['k'], 'o': ['n'], 'n': ['o']}
{'i': ['j', 'k'], 'j': ['i'], 'k': ['i', 'm', 'l'], 'm': ['k'], 'l': ['k'], 'o': ['n'], 'n': ['o']}
Traceback (most recent call last):
File "main.py", line 39, in <module>
undirectedPath(edges, 'k', 'o'); # -> false
File "main.py", line 18, in undirectedPath
return hasPath(graph, nodeA, nodeB)
File "main.py", line 25, in hasPath
if hasPath(graph, neighbor, dst): # True
File "main.py", line 25, in hasPath
if hasPath(graph, neighbor, dst): # True
File "main.py", line 25, in hasPath
if hasPath(graph, neighbor, dst): # True
[Previous line repeated 994 more times]
File "main.py", line 21, in hasPath
if src == dst:
RecursionError: maximum recursion depth exceeded in comparison
** Process exited - Return Code: 1 **
Press Enter to exit terminal
자.. 이제 set() 으로.. 방문 체크 하자.. visited
def buildGraph(edges):
graph = {}
for s, d in edges:
if s not in graph:
graph[s] = []
if d not in graph:
graph[d] = []
graph[s].append(d)
graph[d].append(s)
return graph
def undirectedPath(edges, nodeA, nodeB):
graph = buildGraph(edges)
print(graph)
"""
set() 으로, visited 방문(cycle) 확인
"""
return hasPath(graph, nodeA, nodeB, set())
def hasPath(graph, src, dst, visited):
if src == dst:
return True
"""
# 방문한 노드이므로, 다시 방문할 필요X
"""
if src in visited:
return False
# src 방문 체크
visited.add(src)
for neighbor in graph[src]:
if hasPath(graph, neighbor, dst, visited): # True
return True
return False
edges = [
['i', 'j'],
['k', 'i'],
['m', 'k'],
['k', 'l'],
['o', 'n']
]
print(undirectedPath(edges, 'm', 'j')) # -> true
print(undirectedPath(edges, 'k', 'o')) # -> false
문제 유형3) Connected Components Count 연결된 구성요소의 수
1. 풀이법
1) 우선, 무향 그래프(undirected graph)의 인접 리스트 를 만들어야 함
2) 그리고, 그래프 그림을 그림 그려라!

3) 그래프 섬마다 분리해서, 색을 다르게..

4) 개수 Count => 3개
2. 실제 로직은..
1) 우선, count = 0,
Node 1부터 bfs or dfs 로 검색,
visited 체크

2) 새로운 영역을 순회할때, 그전에 count 를 1증가

3) 다음 검색할 2번 노드로 갔는데, 2번 노드가 visited 방문처리된 노드임.
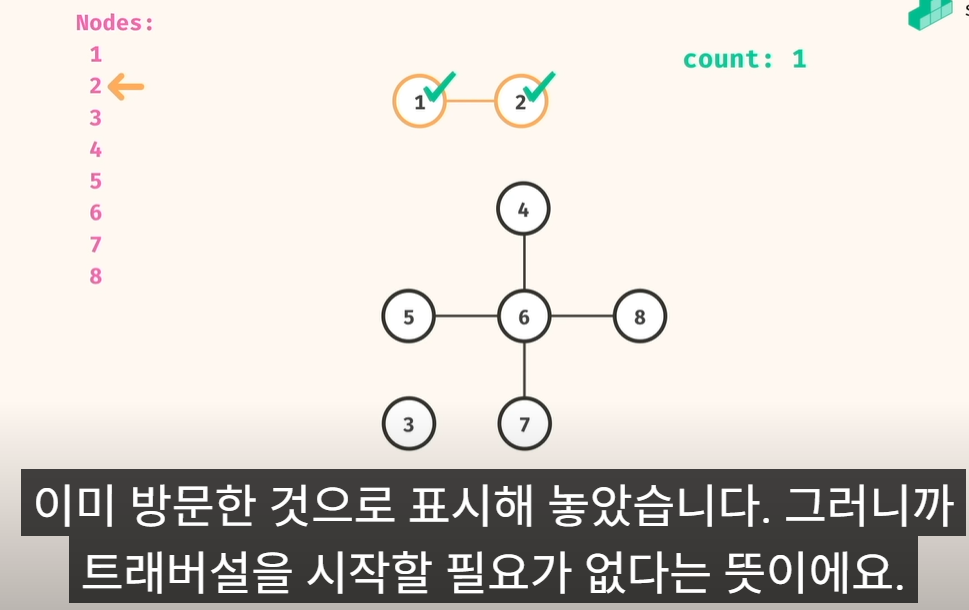
3) 그럼, 그다음 노드인 3번노드로 가서, 검색 시작 하고,
연결된 노드있으면 모두 방문처리해주고,
탐색이 끝나면, count 증가

4) 그럼, 그다음 노드인 4번노드로 가서, 검색 시작 하고,
연결된 노드있으면 모두 방문처리해주고,
탐색이 끝나면, count 증가

복잡도는 시간 및 공간 모두 O(N) 임!!

https://structy.net/problems/connected-components-count
Structy - Learn data structures and algorithms, efficiently.
Structy is the best platform for learning data structures and algorithms. Learn all the topics required for technical interviews through a strong sense of progression with Structy.
structy.net
# Online Python - IDE, Editor, Compiler, Interpreter
def connectedComponentsCount(graph):
visitied = set()
count = 0
for node in graph:
if explore(graph, node, visitied): # True
# 자식까지 모두 탐색끝나면, count 증가
"""
방문한 노드를 탐색했다면,
explore 함수 초반에, 방문검사에서 return False 해서.
여기 조건문 통화 못함
"""
count +=1
return count
def explore(graph, cur, visitied):
# dfs, recusive
if cur in visitied:
return False
# 방문 처리
visitied.add(cur)
for neighbor in graph[cur]:
explore(graph, neighbor, visitied)
# 자식 모두 탐색하고.
return True
print(connectedComponentsCount({
0: [8, 1, 5],
1: [0],
5: [0, 8],
8: [0, 5],
2: [3, 4],
3: [2, 4],
4: [3, 2]
})) # -> 2
문제 유형4) Largest Component
1. 풀이 방법
1) 인접 리스트 가 주어지고..

2) 섬 개수 counting 하고,
각 섬 별로, 사이즈 도.. 계산하고..

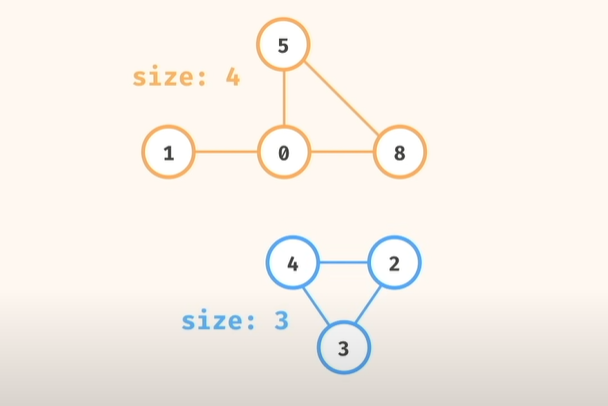
3) lagest component: 4
2. 실제 구현 로직
1) 0 번 노드 부터 탐색(dfs, 재귀 추천)

2) 방문한 노드들은 visited 처리..
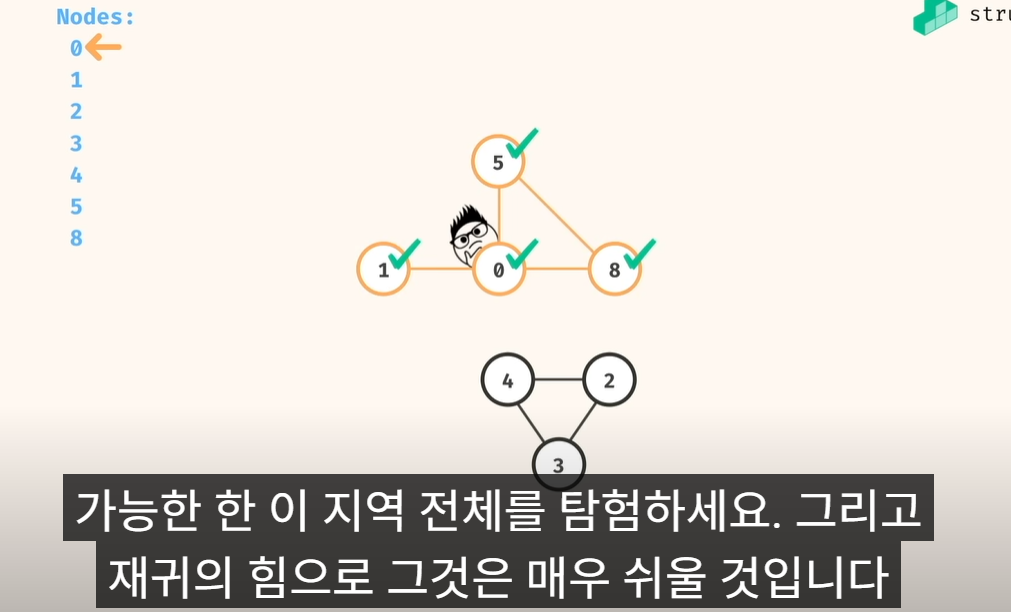
3) 노드 통과할때 count 하는 로직 구현

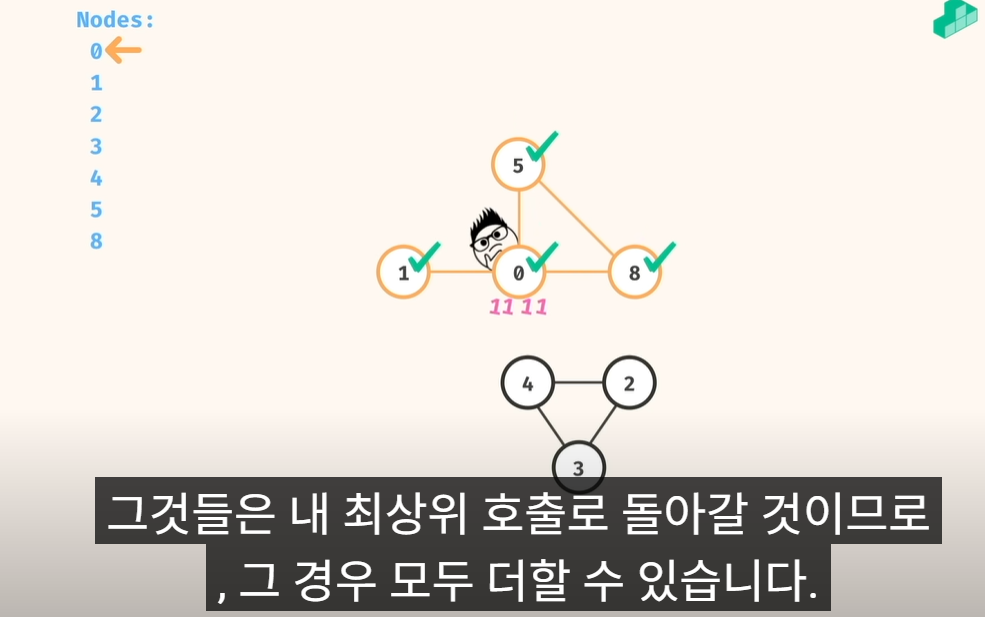

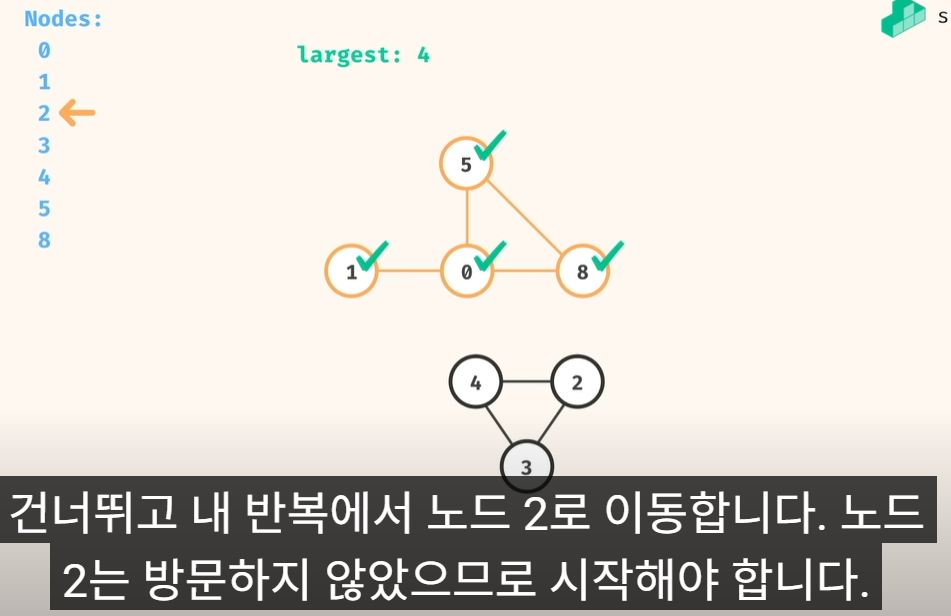
4) 다음 노드 로 이동,
동일하게.. 탐색하면서,
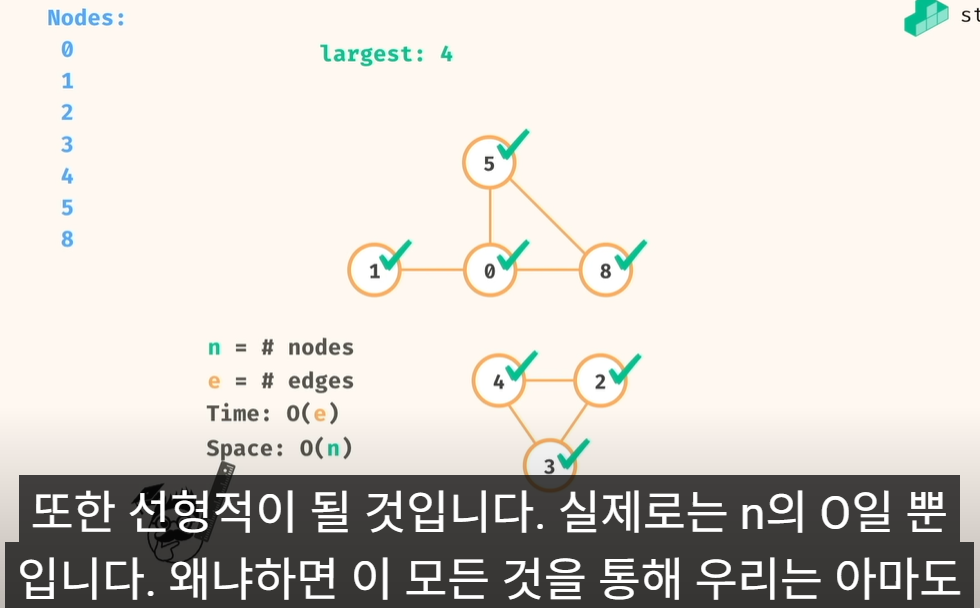
5) 끝까지..가면, count 계산 후 largest 갱신..
복잡도는
https://structy.net/problems/largest-component
Structy - Learn data structures and algorithms, efficiently.
Structy is the best platform for learning data structures and algorithms. Learn all the topics required for technical interviews through a strong sense of progression with Structy.
structy.net
def largestComponent(graph):
visited = set()
longest = 0
for node in graph:
size = exploreSize(graph, node, visited)
if size > longest:
longest = size
return longest
def exploreSize(graph, cur, visited):
if cur in visited:
return 0
# 방문 표시
visited.add(cur)
size = 1 # 현재 노드 개수 추가
for nei in graph[cur]:
# 자식 개수도 누적하게 추가
size += exploreSize(graph, nei, visited)
return size
print(largestComponent({
0: [8, 1, 5],
1: [0],
5: [0, 8],
8: [0, 5],
2: [3, 4],
3: [2, 4],
4: [3, 2]
})) # -> 4
print(largestComponent({
1: [2],
2: [1,8],
6: [7],
9: [8],
7: [6, 8],
8: [9, 7, 2]
})) # -> 6
문제 유형5) 최단 경로 문제. shortest path
1. 풀이법
1) 우선, 에지 edges 목록 (list) 이 주어지고
시작점(src), 도착점(dst) 으로 가는 최단 경로 질문.. 임

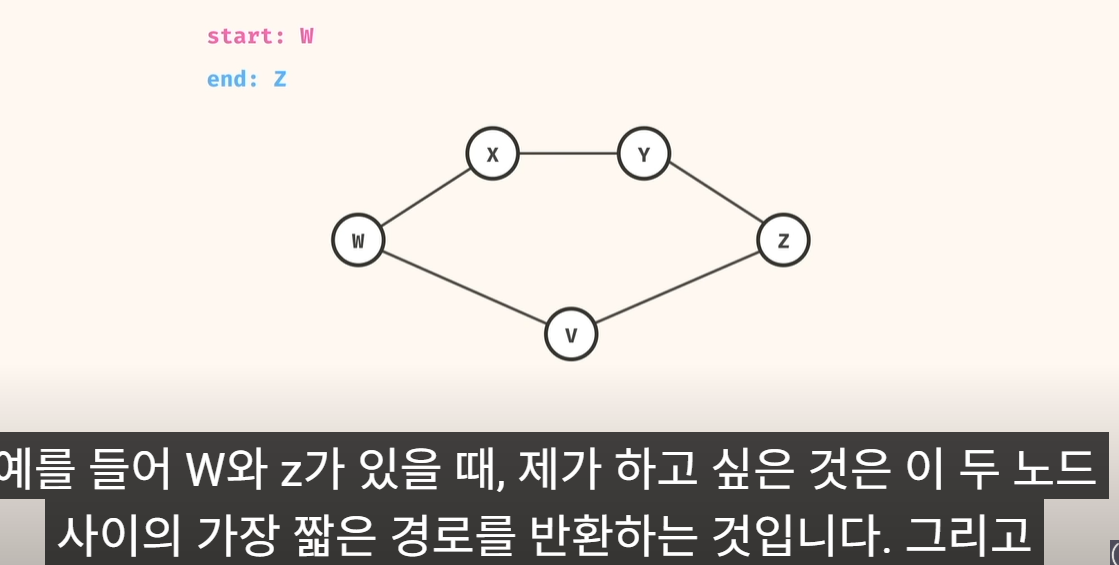
2) 우선, 에지 목록 edges list => adj list 인접 리스트 로 변경
3) path 개수.. count 계산해서..최소값


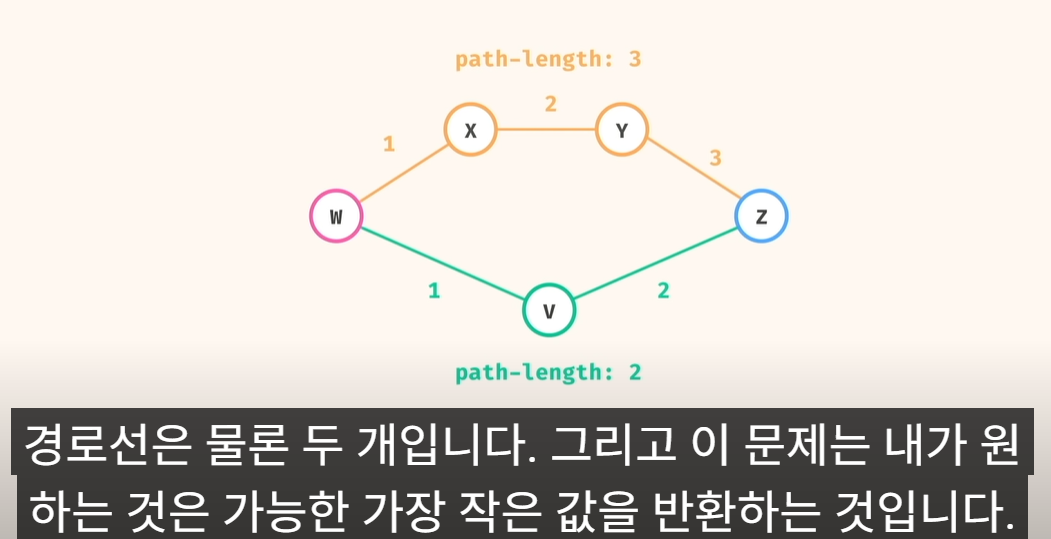
그런데, 어떤 방법으로 찾는것이 좋을까? DFS? BFS?

DFS 의 경우, 처음에 잘못 길을 선택하면.. 엄청 오래 걸림

BFS 의 경우.. 2번만에 찾음 ==> 그래서, 길찾기 문제에서는 BFS 가 훨씬 속도도 빠르고, 효율적임

2. 실제 구현 로직
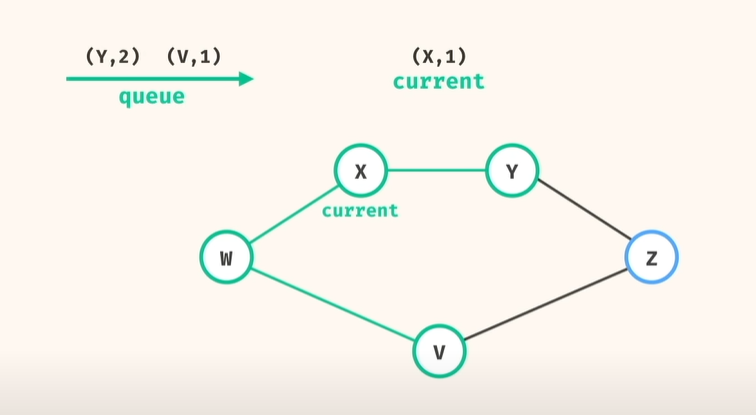
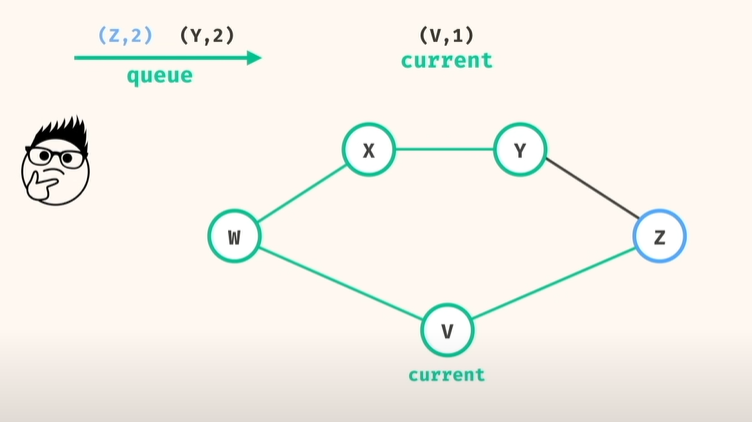
그래서, BFS로 큐 사용 (node, 거리) 해서 풀면
1) 큐 deque 에 (시작점, 시작거리(0)) 추가
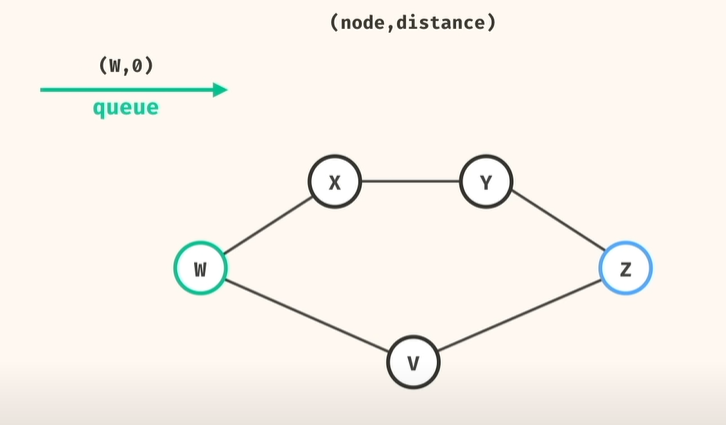
2) 큐에서 꺼내고(popleft) 하고,
이 노드가 dst 인지 아닌지 체크, dst 이면, => 현재 dist 와 비교해서 shortest path 갱신
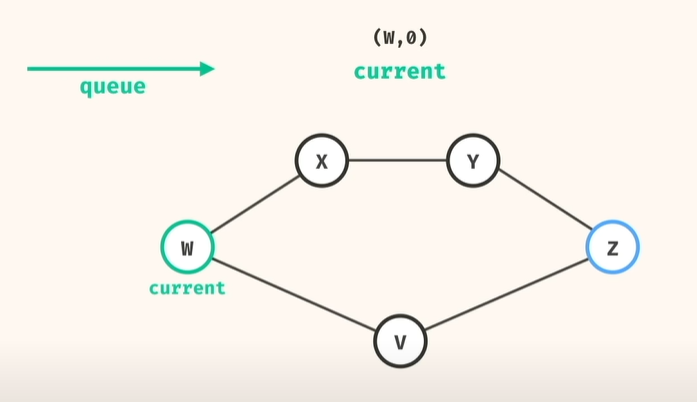
3) 이 노드가 dst 아니면, => 연결된 노드를 다시 큐에 add, 이때 거리를 1더 추가해서..

4) 큐가 빌때까지..반복 가 아니라!!!
제일 먼저 dst 도달한 노드가 나오면, 그게 최단 거리임! 바로 return!!

https://structy.net/problems/shortest-path
Structy - Learn data structures and algorithms, efficiently.
Structy is the best platform for learning data structures and algorithms. Learn all the topics required for technical interviews through a strong sense of progression with Structy.
structy.net
내 코드!! 한번에 품!!
edges1 = [
['w', 'x'],
['x', 'y'],
['z', 'y'],
['z', 'v'],
['w', 'v']
]
edges2 = [
['a', 'c'],
['a', 'b'],
['c', 'b'],
['c', 'd'],
['b', 'd'],
['e', 'd'],
['g', 'f']
]
def buildGraph(edges):
graph = {}
for src, dst in edges:
if not src in graph:
graph[src] = []
if not dst in graph:
graph[dst] = []
graph[src].append(dst)
graph[dst].append(src)
return graph
from collections import deque
def shortestPathBFS(edges, src, dst):
visited = set()
graph = buildGraph(edges)
q = deque([(src, 0)]) # 시작점이니, 거리는 0, tuple 형태로 초기화 해야 함
# visited.add(src)
while q: # 있을때까지 도는데.
cur, dist = q.popleft()
if cur == dst:
return dist
# 방문 체크
if cur in visited:
continue
# 방문 처리
visited.add(cur)
for nei in graph[cur]:
q.append((nei, dist+1)) #tuple 형태로 추가해야 함
return -1
print(shortestPathBFS(edges1, 'w', 'z')) # -> 2
print(shortestPathBFS(edges1, 'y', 'x')) # -> 1
print(shortestPathBFS(edges2, 'e', 'c')) # -> 2
print(shortestPathBFS(edges2, 'b', 'g')) # -> -1
솔루션: visited 처리 루틴이 조금 다름
edges1 = [
['w', 'x'],
['x', 'y'],
['z', 'y'],
['z', 'v'],
['w', 'v']
]
edges2 = [
['a', 'c'],
['a', 'b'],
['c', 'b'],
['c', 'd'],
['b', 'd'],
['e', 'd'],
['g', 'f']
]
def buildGraph(edges):
graph = {}
for src, dst in edges:
if not src in graph:
graph[src] = []
if not dst in graph:
graph[dst] = []
graph[src].append(dst)
graph[dst].append(src)
return graph
from collections import deque
def shortestPathBFS(edges, src, dst):
visited = set()
graph = buildGraph(edges)
q = deque([(src, 0)]) # 시작점이니, 거리는 0, tuple 형태로 초기화 해야 함
visited.add(src) # 시작점 방문 처리
while q: # 있을때까지 도는데.
cur, dist = q.popleft()
if cur == dst:
return dist
for nei in graph[cur]:
if nei not in visited: # 이웃이 방문 안되있어야
visited.add(nei) # 방문 처리
q.append((nei, dist+1)) #tuple 형태로 추가해야 함
return -1
print(shortestPathBFS(edges1, 'w', 'z')) # -> 2
print(shortestPathBFS(edges1, 'y', 'x')) # -> 1
print(shortestPathBFS(edges2, 'e', 'c')) # -> 2
print(shortestPathBFS(edges2, 'b', 'g')) # -> -1
두 버전 모두 동작은 잘 하지만, 효율성과 코드 안정성 측면에서 약간의 차이가 있어요. 아래에 각 방식의 차이점과 어떤 게 더 나은지 비교해 드릴게요.
🔁 두 방식 요약
| 방식 | 방문 체크 위치 | 큐에 넣을 때 방문 처리 여부 | 특이점 |
| A안 (처음 코드) | popleft() 후 visited 검사 | 큐에 넣을 때는 visited.add() 안함 | 중복 방지 로직은 while 안 |
| B안 (개선 코드) | 큐에 넣기 전에 visited 검사 | 큐에 넣을 때 visited.add() 함 | 더 효율적 |
✅ 추천: B안 방식 (큐에 넣을 때 방문 처리)
✔ 이유 1: 불필요한 중복 제거
- A안: 중복 노드가 큐에 여러 번 들어갈 수 있음 → visited 체크로 나중에 걸러냄
- B안: 애초에 큐에 안 들어감 → 큐가 작아져서 성능이 더 좋음
✔ 이유 2: 명확한 방문 처리 위치
- q.append() 하기 전에 visited.add() 를 하는 게 더 안전하고 직관적임
- 특히 경로를 저장하거나 추적할 때 중복 방문을 피하는 구조에 유리함
✔ BFS 시간복잡도 관점
- B안이 탐색 노드 수를 줄여주므로 더 효율적
(특히 그래프 크고 중복 경로 많은 경우에 확실히 차이남)
✨ 정리
- ✅ B안이 더 낫다: q.append() 전에 방문 체크하고 방문 처리도 함께 → 성능과 명확성에서 우위
- ❌ A안도 동작은 하지만 큐에 중복 노드가 들어갈 수 있어 비효율적일 수 있음
🔁 참고: B안 예시
for nei in graph[cur]:
if nei not in visited:
visited.add(nei)
q.append((nei, dist + 1))
문제 유형6) Island Count 섬 개수 문제
1) 육지와 물 격자를 나타내는 2차원 배열이 주어짐
L은 땅, W 는 물임

2) 시각화 => 섬 개수 반환.. 여기서는 4임

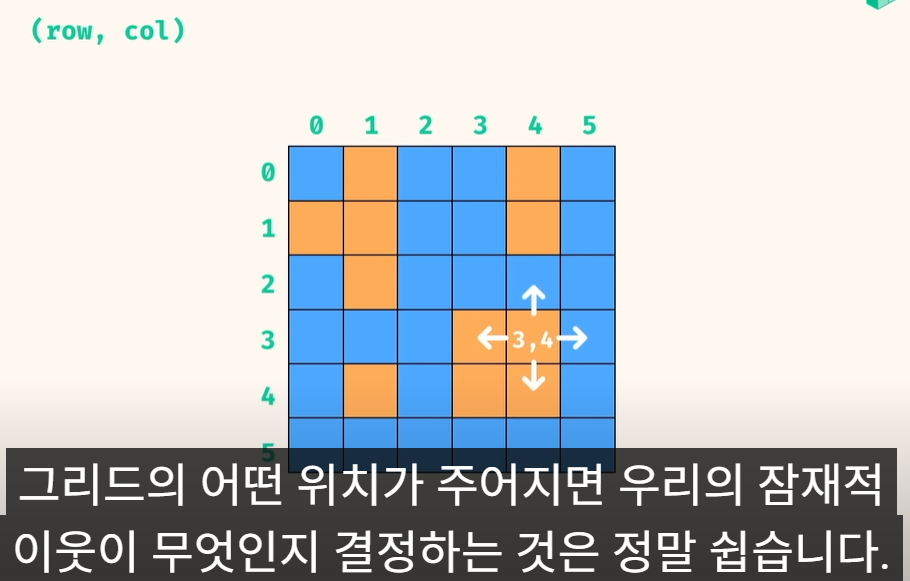
1. 풀이 방법
1) 우선, (r, c) 가 (0,0) 에서 시작, Count =0

2) 그런데, 현재 위치에서 물인지, 육지인지 확인
3) 현재 위치가 물이므로, 다음으로 넘어감 (0,0) -> (0,1)

4) 현재 위치가 땅이므로, visited 로직이 있는 DFS 사용

4) 끝나면, Count 증가 => Count 이제 1
5) 같은 로직으로 r,c 를 증가하면서 동작시키고,
6) 만약, r,c 위치에서 방문한 visited 지점이면, 넘어감
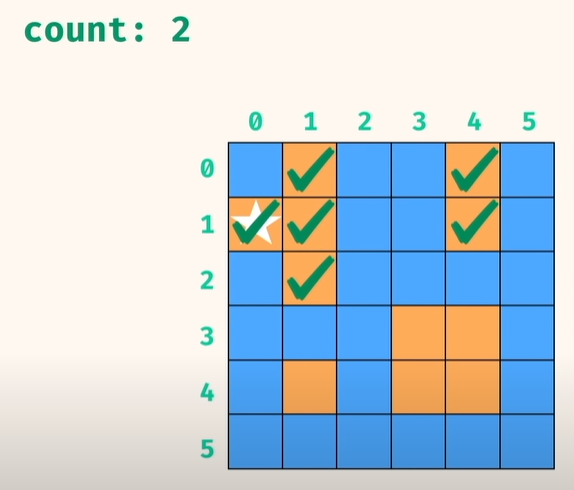
7) 만약, r,c 위치에서 방문하지 않은 지점이면, visited 처리하는 DFS 로 동작하고..
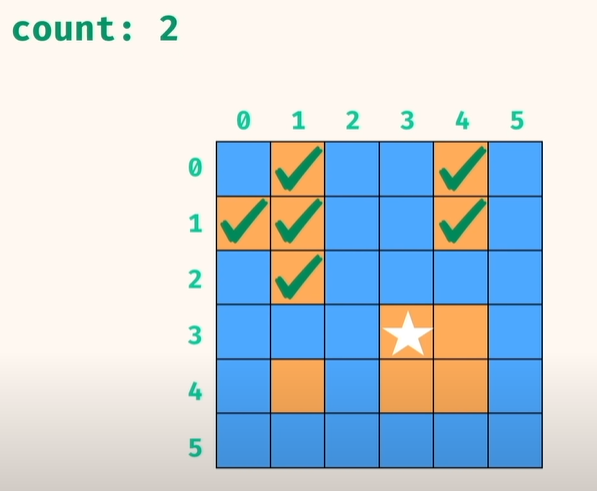


공간 및 시간 복작도는 둘다 O(r*c) 임

https://structy.net/problems/island-count
Structy - Learn data structures and algorithms, efficiently.
Structy is the best platform for learning data structures and algorithms. Learn all the topics required for technical interviews through a strong sense of progression with Structy.
structy.net
내 코드, 한번이 풀림!!
grid1 = [
['W', 'L', 'W', 'W', 'W'],
['W', 'L', 'W', 'W', 'W'],
['W', 'W', 'W', 'L', 'W'],
['W', 'W', 'L', 'L', 'W'],
['L', 'W', 'W', 'L', 'L'],
['L', 'L', 'W', 'W', 'W'],
]
grid2 = [
['L', 'W', 'W', 'L', 'W'],
['L', 'W', 'W', 'L', 'L'],
['W', 'L', 'W', 'L', 'W'],
['W', 'W', 'W', 'W', 'W'],
['W', 'W', 'L', 'L', 'L'],
]
grid3 = [
['L', 'L', 'L'],
['L', 'L', 'L'],
['L', 'L', 'L'],
]
grid4 = [
['W', 'W'],
['W', 'W'],
['W', 'W'],
]
def islandCount(grid):
count = 0
visited = set()
for r in range(len(grid)):
for c in range(len(grid[0])):
if explore(grid, r, c, visited): # True
count +=1
return count
def explore(grid, r, c, visited):
# 그리드 범위내가 아니거나, 방문했거나, 물이면 넘어감
if not (0<= r < len(grid) and 0<= c < len(grid[0])) or (r, c) in visited or grid[r][c] == 'W':
return False
# 방문 추가
visited.add((r, c))
# 4방향 탐색
for dr, dc in [[1,0], [-1,0], [0,1], [0,-1]]:
explore(grid, r+dr, c+dc, visited)
return True
print(islandCount(grid1)) # -> 3
print(islandCount(grid2)) # -> 4
print(islandCount(grid3)) # -> 1
print(islandCount(grid4)) # -> 0
솔루션 : 내 코드와 동일!!
# Online Python - IDE, Editor, Compiler, Interpreter
grid1 = [
['W', 'L', 'W', 'W', 'W'],
['W', 'L', 'W', 'W', 'W'],
['W', 'W', 'W', 'L', 'W'],
['W', 'W', 'L', 'L', 'W'],
['L', 'W', 'W', 'L', 'L'],
['L', 'L', 'W', 'W', 'W'],
]
grid2 = [
['L', 'W', 'W', 'L', 'W'],
['L', 'W', 'W', 'L', 'L'],
['W', 'L', 'W', 'L', 'W'],
['W', 'W', 'W', 'W', 'W'],
['W', 'W', 'L', 'L', 'L'],
]
grid3 = [
['L', 'L', 'L'],
['L', 'L', 'L'],
['L', 'L', 'L'],
]
grid4 = [
['W', 'W'],
['W', 'W'],
['W', 'W'],
]
def islandCount(grid):
count = 0
visited = set()
for r in range(len(grid)):
for c in range(len(grid[0])):
if explore(grid, r, c, visited): # True이면, 섬 탐험이 끝났으므로, count 증가
count +=1
return count
def explore(grid, r, c, visited):
# 그리드 범위내가 아니거나, 방문했거나, 물이면 넘어감
rowInbounds = 0 <= r and r < len(grid)
colInbounds = 0 <= c and c < len(grid[0])
if not rowInbounds or not colInbounds: # 그리드 범위 내 체크를 제일 먼저 해야 함!!
return False
if grid[r][c] == 'W':
return False
if (r, c) in visited:
return False
# 방문 추가
visited.add((r, c))
# 4방향 탐색
explore(grid, r-1, c, visited) # up
explore(grid, r+1, c, visited) # down
explore(grid, r, c-1, visited) # left
explore(grid, r, c+1, visited) # right
return True # 새로운 섬 탐험 끝을 의미
print(islandCount(grid1)) # -> 3
print(islandCount(grid2)) # -> 4
print(islandCount(grid3)) # -> 1
print(islandCount(grid4)) # -> 0
문제 유형7) Minimum Island 최소 섬 문제
똑같이, 2차원 그리드가 주어지고,
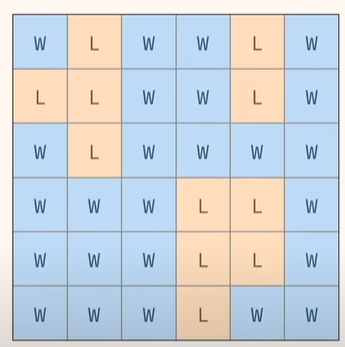
최소 섬 크기를 반환
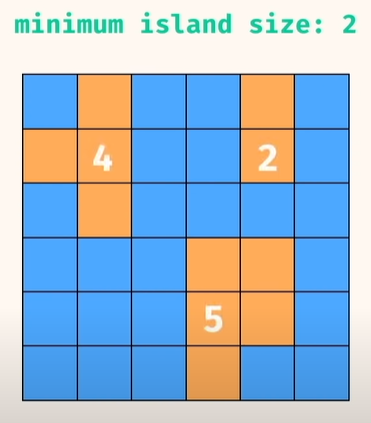
1. 풀이법
1) 이전 섬 개수 구하는 로직과 거의 비슷하되,
근접 loop, DFS 로직 (visited)



2) 최상위 호출에서 return True 가 아니라, 섬 크기를 구해서 return 하면 됨
3) minSize 와 섬 크기를 비교해서, 최소값 갱신
4) 그리고, 계속 동일하게..
시간 공간 복잡도: O(rc)

https://structy.net/problems/minimum-island
Structy - Learn data structures and algorithms, efficiently.
Structy is the best platform for learning data structures and algorithms. Learn all the topics required for technical interviews through a strong sense of progression with Structy.
structy.net
★ 내 코드 == 솔루션 코드 ★
grid1 = [
['W', 'L', 'W', 'W', 'W'],
['W', 'L', 'W', 'W', 'W'],
['W', 'W', 'W', 'L', 'W'],
['W', 'W', 'L', 'L', 'W'],
['L', 'W', 'W', 'L', 'L'],
['L', 'L', 'W', 'W', 'W'],
]
grid2 = [
['L', 'W', 'W', 'L', 'W'],
['L', 'W', 'W', 'L', 'L'],
['W', 'L', 'W', 'L', 'W'],
['W', 'W', 'W', 'W', 'W'],
['W', 'W', 'L', 'L', 'L'],
]
grid3 = [
['L', 'L', 'L'],
['L', 'L', 'L'],
['L', 'L', 'L'],
]
grid4 = [
['W', 'W'],
['L', 'L'],
['W', 'W'],
['W', 'L']
]
def minimumIsland(grid):
visited = set()
minSize = float("inf")
for r in range(len(grid)):
for c in range(len(grid[0])):
size = exploreSize(grid, r, c, visited)
"""
섬이 아닌 지역에서는 size 가 0 이 반환되므로
사이즈가 0 이상일때만, 비교해야 함
"""
if size:
minSize = min(minSize, size)
return minSize
def exploreSize(grid, r, c, visited):
rowInbounds = 0 <= r and r < len(grid)
colInbounds = 0 <= c and c < len(grid[0])
# 기본적으로 사이즈를 반환해야하는데,
# 아래 조건 3개는 다른 개수 카운팅을 안할거기 때문에.
# 아무 영향을 줄수 없는 0을 반환해야 함.
if not rowInbounds or not colInbounds: # 범위를 벗어나면
return 0
if grid[r][c] == 'W': # 물이면
return 0
if (r, c) in visited: # 이미 방문했으면
return 0
# 방문 처리
visited.add((r, c))
"""
!! 여기서 부터가 핵심!!
사이즈 1로, 초기화, 계속 더함. 그리고 사이즈 반환
"""
size = 1 # 기본값은, 내거 포함해야하므로, 1로.
# 4가지 이웃 방문 하면서, size 계속 증가..
size += exploreSize(grid, r-1, c, visited)
size += exploreSize(grid, r+1, c, visited)
size += exploreSize(grid, r, c-1, visited)
size += exploreSize(grid, r, c+1, visited)
return size
print(minimumIsland(grid1)) # -> 2
print(minimumIsland(grid2)) # -> 1
print(minimumIsland(grid3)) # -> 9
print(minimumIsland(grid4)) # -> 1★ 여러우니.. 연습 필요!! ★
'Coding Test > 알고리즘 이론' 카테고리의 다른 글
| DP 이론 (0) | 2025.04.28 |
|---|---|
| 순열(permutaion) 과 조합(combination) (0) | 2025.04.16 |
| [DP: LCS 최장 공통 부분수열 Longest Common Subsequence] (0) | 2025.04.14 |
| DP: Unbounded Knapsack (0) | 2025.04.13 |
| [DP] 0/1 Knapsack 문제: 최대 profit 가지는 가방 선택 문제 ★★★ (0) | 2025.04.12 |