Gradient Descent 경사 하강법

Gradient Descent

Easy

Your task is to minimize the function via Gradient Descent: f(x)=x2f(x)=x2.

Gradient Descent is an optimization technique widely used in machine learning for training models. It is crucial for minimizing the cost or loss function and finding the optimal parameters of a model.

For the above function the minimizer is clearly x = 0, but you must implement an iterative approximation algorithm, through gradient descent.

Input:

• iterations - the number of iterations to perform gradient descent. iterations >= 0.
• learning_rate - the learning rate for gradient descent. 1 > learning_rate > 0.
• init - the initial guess for the minimizer. init != 0.

Given the number of iterations to perform gradient descent, the learning rate, and an initial guess, return the value of x that globally minimizes this function.

Round your final result to 5 decimal places using Python's round() function.

Example 1:

Input: 
iterations = 0, learning_rate = 0.01, init = 5

Output:
5

 

Example 2:

Input: 
iterations = 10, learning_rate = 0.01, init = 5

Output:
4.08536

 

🧮 문제 설명: Gradient Descent로 함수 최소값 찾기

🎯 목표

주어진 함수 

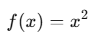
를 Gradient Descent (경사 하강법) 을 사용하여 최소화하는 문제입니다.

---

🧠 Gradient Descent란?

Gradient Descent는 머신러닝에서 모델을 최적화할 때 자주 사용되는 알고리즘입니다.
주어진 함수의 기울기(미분값)를 이용해, 최소값이 나오는 지점을 반복적으로 찾아가는 방식입니다.

---

✅ 입력값

세 가지 값이 주어집니다:

1. iterations (정수):
   Gradient Descent를 몇 번 반복할지 결정합니다.
   • 조건: iterations >= 0
2. learning_rate (실수):
   한 번 이동할 때 얼마나 이동할지 정하는 값입니다.
   • 조건: 0 < learning_rate < 1
3. init (실수):
   시작점, 즉 x의 초기값입니다.
   • 조건: init != 0 (0이면 이미 최소값이므로 의미 없음)

---

📤 출력값

반복 후 얻어진 xxx 값을 소수점 다섯 자리까지 반올림해서 반환합니다.

Round your final result to 5 decimal places using Python's round() function.

 

class Solution:
    def get_minimizer(self, iterations: int, learning_rate: float, init: int) -> float:
        # 초기값 x 설정 (초기 추정값)
        x = init

        # 설정한 반복 횟수만큼 경사 하강법을 수행
        for _ in range(iterations):
            # 함수 f(x) = x^2의 도함수는 f'(x) = 2x 이므로, 현재 x에서의 기울기(gradient)는 2x
            gradient = 2 * x

            # 경사 하강법 공식: x = x - learning_rate * gradient
            # 기울기 방향의 반대 방향으로 learning_rate 만큼 이동
            x -= learning_rate * gradient

        # 최종적으로 얻어진 x 값을 소수점 5자리까지 반올림하여 반환
        return round(x, 5)