https://youtu.be/XYi2-LPrwm4?si=8R5kcaUc9tWO8sSQ






초기값 세팅 설명

초기 설정의 의미
- 첫 번째 행과 열은 문자열이 비어 있을 때 작업의 기준점을 제공합니다.
- 이후, 이 값을 기반으로 나머지 테이블 값을 채우며 두 문자열의 변환 비용을 계산합니다.
이후 과정

결론
DP 테이블의 최종 값은 문자열을 변환하는 모든 가능한 경로를 고려해 최적의 변환 비용을 계산한 결과입니다. 이를 통해 삽입, 삭제, 교체 작업을 효율적으로 비교할 수 있습니다.
Code
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
# DP 테이블 생성
# cache[i][j]: word1[i:]를 word2[j:]로 변환하는 최소 작업 수
cache = [[float("inf")] * (len(word2) + 1) for i in range(len(word1) + 1)]
# 초기값 설정
# word1이 비어 있는 경우: word2[j:]로 변환하기 위해 삽입만 필요
for j in range(len(word2) + 1):
cache[len(word1)][j] = len(word2) - j # 남은 글자 수만큼 삽입
# word2가 비어 있는 경우: word1[i:]를 비우기 위해 삭제만 필요
for i in range(len(word1) + 1):
cache[i][len(word2)] = len(word1) - i # 남은 글자 수만큼 삭제
# DP 테이블 계산
# 역순으로 계산: word1[i:]와 word2[j:]를 고려
for i in range(len(word1) - 1, -1, -1): # word1의 끝에서 시작
for j in range(len(word2) - 1, -1, -1): # word2의 끝에서 시작
if word1[i] == word2[j]: # 두 문자가 같으면 작업 필요 없음
cache[i][j] = cache[i + 1][j + 1]
else: # 삽입, 삭제, 교체 중 최소 작업 선택
cache[i][j] = 1 + min(
cache[i + 1][j], # 삭제: word1[i] 삭제
cache[i][j + 1], # 삽입: word2[j] 삽입
cache[i + 1][j + 1] # 교체: word1[i]를 word2[j]로 교체
)
# 최종 결과: word1[0:]를 word2[0:]로 변환하는 최소 작업 수
return cache[0][0]
# 예제 실행
solution = Solution()
print(solution.minDistance("horse", "ros")) # 출력: 3
print(solution.minDistance("intention", "execution")) # 출력: 5
아래 코드로..
https://youtu.be/dY_dZohgVa8?si=DGLuMiDNJzl1cj1P
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
len1 = len(word1)
len2 = len(word2)
# 배열 만들기
# 결국 답은 dp[len1][len2]
"""
i 는 1부터 len1 = len(word1) 까지
j 는 1부터 len2 = len(word2) 까지
d[i][j]
word1 의 i 까지의 부분 문자열을
word2 의 j 까지의 부분 문자열로
교체하기 위한 최소 작업 수
문자열이 abs -> def 로 주어질때
d[1][1] 은
a->d, 즉, a 를 d로 바꾸기 위한 최소 작업수: 1
"""
# 배열 생성, +1 꼭 필요
# 배열 생성시, len1, len2 순서 중요!
# dp = ([0]*(len2+1)) *(len1+1) <- 이건 2차원 배열 아님
dp = [[0] * (len2 + 1) for _ in range(len1 + 1)]
# 초기화
# i: word1 의 부분 문자열 이고
# j: 0 즉, "" 공백 문자열. 이었을때
# 첫번째 문자열을 공백으로 교체하기 위한 최소 작업수
# 첫번째 문자열의 단어 길이만큼 필요
# word1 = "horse" 이면
# dp[1][0] 은 'h' 와 공백 -> 1글자를 공백으로 -> 작업수 1번 필요
# dp[2][0] 은 'ho' 와 공백 -> 2글자를 공백으로 -> 작업수 2번 필요
# dp[3][0] 은 'hor' 와 공백 -> 3글자를 공백으로 -> 작업수 3번 필요
# .. 이런식
for i in range(len1 + 1): # 초기화는 +1 꼭 필요
dp[i][0] = i
# j: word2 의 부분 문자열
for j in range(len2 + 1):
dp[0][j] = j
# 루프: 1부터 ~ *주의*
for i in range(1, len1+1):
for j in range(1, len2+1):
if word1[i-1] == word2[j-1]:
# word1의 i번째 문자와 word2의 j번째 문자가 같으면,
# 메모이제이션 배열에서 대각선 위의 값을 가져오면 됨
# 왜냐면, 문자가 같기때문에, 어떤 오퍼레이션이 추가로 필요없음
# 그래서, 그 전의 i-1, j-1의 값이 그대로 i,j 값이 됨
dp[i][j] = dp[i-1][j-1]
else:
# 문자가 다르면
# 추가 작업인
# insert, delete, replace 중 하나가 필요하니, 작업이 1 더 더해짐
dp[i][j] = min(dp[i-1][j-1], dp[i][j-1], dp[i-1][j]) + 1
# 리턴: 마지막..값으로.. *주의*
return dp[len1][len2]
https://youtu.be/6jvSfC2-JDo?si=R2jXQFFVxaokuPBW
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
M, N = len(word1), len(word2)
dp = [[0] * (N+1) for _ in range(M+1)] # +1 주의
for m in range(M+1): # +1 주의
dp[m][0] = m
for n in range(N+1): # +1 주의
dp[0][n] = n
for m in range(1, M+1): # 1부터 주의
for n in range(1, N+1): # 1부터 주의
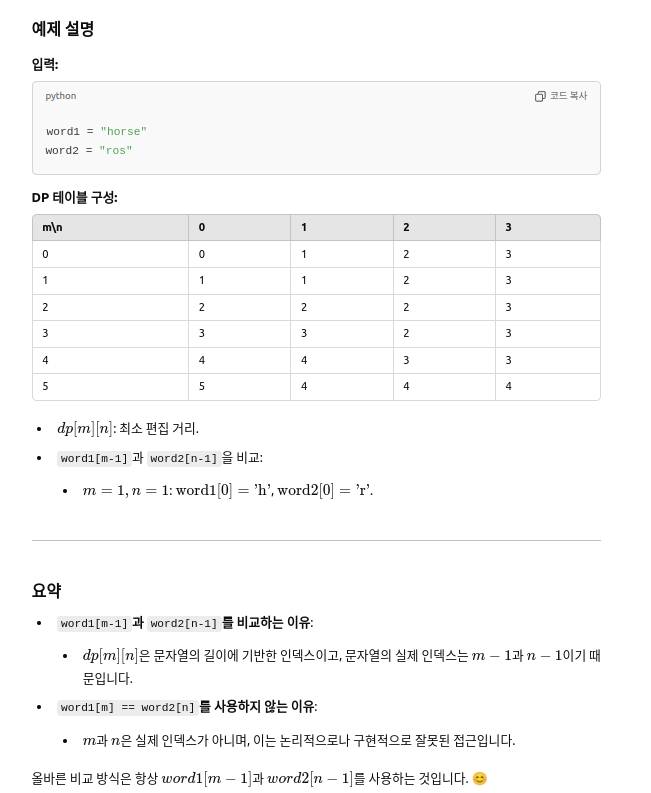
"""
문자열의 실제 인덱스는 0부터 시작하지만,
DP 테이블은 1부터 시작하도록 설정됨
따라서, dp[m][n]은 문자열의 실제 인덱스 m−1과 n−1을 참조함
"""
if word1[m-1] == word2[n-1]: # 왜 -1??
dp[m][n] = dp[m-1][n-1]
else:
dp[m][n] = min(dp[m-1][n-1], dp[m][n-1], dp[m-1][n]) + 1
return dp[M][N]

최종 코드
주어진 두 문자열 word1, word2를 서로 같게 만들기 위한 최소 연산 횟수를 구하는 문제예요.
🎯 문제 설명
✅ 목표:
- 문자열 word1을 삽입(insert), 삭제(delete), 교체(replace) 연산으로 문자열 word2로 바꾸는 최소 횟수를 구하세요.
📘 예시
word1 = "horse"
word2 = "ros"
변환 과정 (예시):
- horse → orse (delete 'h')
- orse → rse (replace 'o' → 'r')
- rse → ros (replace 'e' → 's')
✔ 총 3회 → 정답: 3
✅ 핵심 개념: dp[i][j]의 의미
| dp[i][j] | word1[0:i]을 word2[0:j]로 바꾸는 데 필요한 최소 연산 횟수 |
🔄 점화식 설명
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1] # 문자가 같으면 연산 필요 없음
else:
dp[i][j] = 1 + min(
dp[i-1][j], # 삭제 (delete word1[i-1])
dp[i][j-1], # 삽입 (insert word2[j-1])
dp[i-1][j-1] # 교체 (replace word1[i-1] → word2[j-1])
)
"""
1) word1의 이전꺼(i-1)까지 문자열로 word2의 현재(j) 문자열 만들수 있으니,
word1의 현재(i) 문자 삭제 => dp[i-1][j]
2) word1의 현재(i)까지 문자열로 word2의 이전꺼(j-1)까지의 문자열 만들수 있으니,
word2에 문자 하나더 추가 => dp[i][j-1]
3) 이전꺼 까지는 둘다 같으니, 이번에 나온 문자는 둘다 교체. ==> dp[i-1][j-1]
"""✅ 전체 코드 + 상세 주석
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
M, N = len(word1), len(word2)
# dp[i][j]는 word1[0:i] → word2[0:j]로 바꾸는 최소 연산 횟수
dp = [[0] * (N + 1) for _ in range(M + 1)]
# 초기화: word1을 비우는 경우 (삭제만 필요)
for i in range(M + 1):
dp[i][0] = i # i번 삭제
# 초기화: word2를 만들기 위해 삽입만 필요한 경우
for j in range(N + 1):
dp[0][j] = j # j번 삽입
# 점화식 적용
for i in range(1, M + 1):
for j in range(1, N + 1):
if word1[i - 1] == word2[j - 1]:
# 현재 문자가 같으면, 연산 없이 그대로 유지 가능
dp[i][j] = dp[i - 1][j - 1]
else:
# 문자가 다르면, 3가지 중 최소 선택 + 1 (이번 연산 포함)
dp[i][j] = 1 + min(
dp[i][j - 1], # 삽입: word2[j-1] 추가
dp[i - 1][j], # 삭제: word1[i-1] 제거
dp[i - 1][j - 1] # 교체: word1[i-1] → word2[j-1]
)
# 최종 결과: word1[0:M] → word2[0:N] 최소 연산 수
return dp[M][N]🧾 시간 및 공간 복잡도
| 시간 | O(M × N) |
| 공간 | O(M × N) (→ 공간 최적화하면 O(N) 가능) |
✅ 요약
| 조건 | 연산 | 설명 |
| word1[i-1] == word2[j-1] | 0 | 그대로 넘어감 |
| 다름 | 1 + min(...) | 삽입, 삭제, 교체 중 최소 선택 |
'job 인터뷰 > 코테(Amazon) 준비' 카테고리의 다른 글
| 253. Meeting Rooms II ☆★★★★ (0) | 2025.05.02 |
|---|---|
| 347. Top K Frequent Elements ★★★★★ (0) | 2025.04.18 |
| 122. Best Time to Buy and Sell Stock II ★★★★★ (0) | 2024.11.26 |
| BST: 875. Koko Eating Bananas ☆★★ (3) | 2024.11.22 |