[Two Pointers] 42. Trapping Rain Water ★★★

LeetCode/NeetCode

[Two Pointers] 42. Trapping Rain Water ★★★

hyunkookim 2024. 11. 28. 14:43

https://youtu.be/ZI2z5pq0TqA?si=vMNp4_SRqkju2a6b

O(n) 공간 사용

from typing import List

class Solution:
    def trap(self, height: List[int]) -> int:
        # 높이 배열의 길이를 가져옵니다.
        n = len(height)
        # 배열이 비어있는 경우 0을 반환 (예외 처리)
        if not n:
            return 0

        # maxLeft: 각 위치에서 왼쪽으로 가장 높은 기둥의 높이를 저장할 리스트
        # maxRight: 각 위치에서 오른쪽으로 가장 높은 기둥의 높이를 저장할 리스트
        # minLR: 각 위치에서 maxLeft와 maxRight 중 작은 값을 저장할 리스트
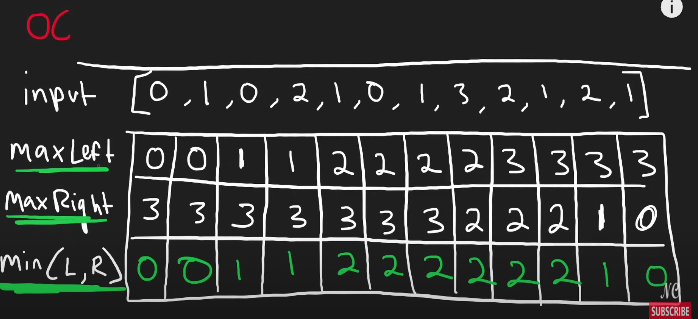
        maxLeft, maxRight, minLR = [0] * n, [0] * n, [0] * n

        # maxLeft의 첫 번째 값은 첫 번째 기둥의 높이로 초기화
        maxLeft[0] = height[0]
        # maxRight의 마지막 값은 마지막 기둥의 높이로 초기화
        maxRight[n-1] = height[n-1]

        # 왼쪽에서 오른쪽으로 순회하며 maxLeft 값을 계산
        for i in range(1, n):
            # 현재 위치의 maxLeft는 이전 위치의 maxLeft와 바로 이전 기둥의 높이 중 큰 값
            maxLeft[i] = max(maxLeft[i-1], height[i-1])

        # 오른쪽에서 왼쪽으로 순회하며 maxRight 값을 계산
        for i in range(n-2, -1, -1):
            # 현재 위치의 maxRight는 다음 위치의 maxRight와 바로 다음 기둥의 높이 중 큰 값
            maxRight[i] = max(maxRight[i+1], height[i+1])

        # 최종적으로 담길 수 있는 빗물의 양을 계산하기 위한 변수
        res = 0
        # 각 위치에서 빗물의 양을 계산
        for i in range(n):
            # minLR: maxLeft와 maxRight 중 작은 값을 저장
            minLR[i] = min(maxLeft[i], maxRight[i])
            # 빗물의 양은 minLR에서 현재 기둥 높이를 뺀 값
            sub = minLR[i] - height[i]
            # 빗물이 양수일 때만 결과에 더해줌 (음수는 빗물이 담기지 않는 경우)
            res += sub if sub >= 0 else 0 

        # 최종적으로 계산된 빗물의 양 반환
        return res

O(1) 공간 사용

from typing import List

class Solution:
    def trap(self, height: List[int]) -> int:
        # 투 포인터를 사용하여 빗물의 양을 계산
        l, r = 0, len(height) - 1  # 왼쪽 포인터 l과 오른쪽 포인터 r 초기화
        leftMax, rightMax = height[l], height[r]  # 왼쪽과 오른쪽에서 가장 높은 기둥의 초기값 설정
        res = 0  # 최종적으로 담길 빗물의 양을 저장할 변수

        # 왼쪽 포인터가 오른쪽 포인터를 넘기 전까지 반복
        while l < r:
            # 왼쪽 최대값이 오른쪽 최대값보다 작은 경우
            if leftMax < rightMax:
                l += 1  # 왼쪽 포인터 이동
                leftMax = max(leftMax, height[l])  # 새로운 leftMax 갱신
                res += leftMax - height[l]  # 빗물의 양은 leftMax와 현재 높이의 차이
            else:
                # 오른쪽 최대값이 왼쪽 최대값보다 작거나 같은 경우
                r -= 1  # 오른쪽 포인터 이동
                rightMax = max(rightMax, height[r])  # 새로운 rightMax 갱신
                res += rightMax - height[r]  # 빗물의 양은 rightMax와 현재 높이의 차이

        # 최종적으로 계산된 빗물의 양 반환
        return res

주석 설명

투 포인터 초기화:
- l은 왼쪽 끝에서 시작하고, r은 오른쪽 끝에서 시작합니다.
- leftMax와 rightMax는 각각 왼쪽과 오른쪽에서 현재까지의 최대 기둥 높이를 추적합니다.
반복문 로직:
- leftMax < rightMax인 경우, 더 낮은 쪽(leftMax)에서 빗물을 계산하며 왼쪽 포인터를 이동합니다.
- 반대로, rightMax가 작거나 같은 경우 오른쪽에서 빗물을 계산하며 오른쪽 포인터를 이동합니다.
- 이 방식은 항상 낮은 쪽에서 빗물을 계산하므로 각 단계에서 불필요한 비교를 줄이고 효율적으로 계산할 수 있습니다.
빗물 계산:
- 현재 높이(height[l] 또는 height[r])가 최대값(leftMax 또는 rightMax)보다 작다면, 최대값과 현재 높이의 차이가 해당 위치에서 담길 수 있는 빗물의 양입니다.
반복 종료 조건:
- 왼쪽 포인터가 오른쪽 포인터를 넘어가면 모든 위치에서의 빗물 계산이 완료됩니다.

최종 코드

DP 로직

class Solution:
    def trap(self, height: List[int]) -> int:
        # 현재 위치 i에서 고인 물의 양 =
        # min(왼쪽에서의 최대 높이, 오른쪽에서의 최대 높이) - 현재 위치의 높이

        lenH = len(height)
        maxLeftH = [0] * lenH   # 각 위치에서 왼쪽 방향으로의 최대 높이 저장
        maxRightH = [0] * lenH  # 각 위치에서 오른쪽 방향으로의 최대 높이 저장

        # 왼쪽 최대 높이 배열 채우기
        for l in range(1, lenH):
            # 현재 위치 l의 왼쪽까지 중에서 가장 높은 높이를 저장
            maxLeftH[l] = max(maxLeftH[l - 1], height[l - 1])

        # 오른쪽 최대 높이 배열 채우기
        for r in range(lenH - 2, -1, -1):  # 오른쪽에서 왼쪽으로 이동
            # 현재 위치 r의 오른쪽까지 중에서 가장 높은 높이를 저장
            maxRightH[r] = max(maxRightH[r + 1], height[r + 1])

        area = 0  # 고인 물의 총량

        # 각 위치에서 고인 물의 양 계산
        for i in range(lenH):
            # 현재 위치에 고일 수 있는 물의 높이 계산
            curDrop = min(maxLeftH[i], maxRightH[i]) - height[i]
            # 고인 물이 0보다 크면 더해줌 (음수인 경우는 고이지 않음)
            area += curDrop if curDrop > 0 else 0

        return area  # 총 고인 물의 양 반환

✅ 요약 정리

왼쪽/오른쪽 최대 높이 배열을 먼저 채워서,
각 위치에서 고일 수 있는 최대 물 높이를 계산함.
시간 복잡도: O(n)
공간 복잡도: O(n) (두 개의 보조 배열 사용)

좋아요! 위에서 작성하신 DP 방식과 **같은 로직(= min(왼쪽 최대, 오른쪽 최대) - 현재 높이)**을 사용하지만,
보조 배열 없이 공간을 줄이는 투 포인터(two-pointer) 버전을 아래에 설명해드릴게요.

✅ 투 포인터 버전 (O(n) 시간, O(1) 공간)

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height:
            return 0

        l, r = 0, len(height) - 1       # 왼쪽, 오른쪽 포인터
        left_max, right_max = 0, 0      # 각 방향에서 현재까지의 최대 높이
        area = 0                        # 고인 물의 총량

        while l < r:
            if height[l] < height[r]:
                # 왼쪽이 더 낮으면, 왼쪽 기준으로 물 높이 계산
                if height[l] >= left_max:
                    left_max = height[l]    # 왼쪽 최대 높이 갱신
                else:
                    area += left_max - height[l]  # 물이 고임
                l += 1
            else:
                # 오른쪽이 더 낮으면, 오른쪽 기준으로 물 높이 계산
                if height[r] >= right_max:
                    right_max = height[r]   # 오른쪽 최대 높이 갱신
                else:
                    area += right_max - height[r]  # 물이 고임
                r -= 1

        return area

투 포인터 방식에서 left_max나 right_max를 갱신하는 경우에는 왜 area(고인 물 양)을 계산하지 않는지 설명해드릴게요.

✅ 핵심 개념:

고인 물 = max 높이 - 현재 높이
이때, 고인 물이 생기려면 "현재 높이 < max 높이" 여야 함.

🔍 왜 left_max 갱신할 때는 area 계산을 안 할까?

height[l] >= left_max라는 건:

현재 위치가 지금까지 본 가장 높은 막대거나,
최소한 지금까지 본 막대들보다 더 높기 때문에
👉 물이 고일 수 없는 위치라는 뜻이에요.

✅ 예를 들어:

left_max = 2
height[l] = 3
→ 이제 left_max를 3으로 갱신해야 하지만, → left_max - height[l] = 3 - 3 = 0 → 물이 고일 수 없음
→ 그래서 area 계산 생략

✅ 로직 요약 (→ DP 배열 없이도 같은 개념 사용)

left_max, right_max는 각각 현재까지의 왼쪽/오른쪽 최대 높이를 저장함.
height[l] < height[r]인 경우:
- 왼쪽 막대 기준으로 고일 수 있는 물을 계산.
height[r] <= height[l]인 경우:
- 오른쪽 막대 기준으로 고일 수 있는 물을 계산.
이 과정을 포인터가 만날 때까지 반복.

그래서, 다시 말하면 이렇게 해도 됨.

결국. 갱신할때는 area 값이 0 이 되서, 실행안한것처럼 됨

class Solution:
    def trap(self, height: List[int]) -> int:
        # 현재 위치 i 에서의 고인 물 양은
        # = min(좌측 최대 높이, 우측 최대 높이) - 현재 높이

        lenH = len(height)
        l, r = 0, lenH - 1      # 왼쪽 포인터, 오른쪽 포인터
        area = 0                # 총 고인 물의 양
        maxL, maxR = 0, 0       # 현재까지의 왼쪽/오른쪽 최대 높이

        while l < r:
            if height[l] < height[r]:
                # 왼쪽 막대가 더 낮으면 왼쪽 기준으로 판단
                maxL = max(maxL, height[l])  # 왼쪽 최대 높이 갱신
                # 현재 위치에 고일 수 있는 물 = maxL - 현재 높이
                area += max(maxL - height[l], 0)
                l += 1
            else:
                # 오른쪽 막대가 더 낮거나 같으면 오른쪽 기준으로 판단
                maxR = max(maxR, height[r])  # 오른쪽 최대 높이 갱신
                # 현재 위치에 고일 수 있는 물 = maxR - 현재 높이
                area += max(maxR - height[r], 0)
                r -= 1

        return area

✅ 로직 핵심 요약

작은 쪽을 기준으로 고인 물을 계산해야 안전함.
왜냐하면 min(maxL, maxR)이 작은 쪽으로 결정되기 때문!
따라서 작은 쪽의 max 값을 갱신하면서 고인 물을 누적 계산.

✅ 시간 & 공간 복잡도

시간 복잡도: O(n) (포인터 한 번씩만 이동)
공간 복잡도: O(1) (추가 배열 사용 안 함)

✅ 장점 비교

방식	시간 복잡도	공간 복잡도	특징
DP 배열 방식	O(n)	O(n)	코드가 직관적이고 이해 쉬움
투 포인터	O(n)	O(1)	공간 효율적, 최적화된 방식

'LeetCode > NeetCode' 카테고리의 다른 글

[Two Pointers] 167. Two Sum II - Input Array Is Sorted (0)	2024.11.29
[Two Pointers] 125. Valid Palindrome (1)	2024.11.28
[Two Pointers] 80. Remove Duplicates from Sorted Array II (0)	2024.11.25
BST: 374. Guess Number Higher or Lower ★ (0)	2024.11.19
Graphs: 994. Rotting Oranges ★★★ (0)	2024.11.19

현재글[Two Pointers] 42. Trapping Rain Water ★★★

hyunkookim 님의 블로그

hyunkookim 님의 블로그 입니다.

BFS, 오블완, array / string, Coding Test, BST, 누적합, 티스토리챌린지, 슬라이딩윈도우, Backtracking, 우선순위큐, tree, heap, LeetCode, leetcode75, neetcode150, top150, neetcode, dfs, dp, Two pointers,

Today :
Yesterday :

hyunkookim 님의 블로그