hyunkookim 님의 블로그

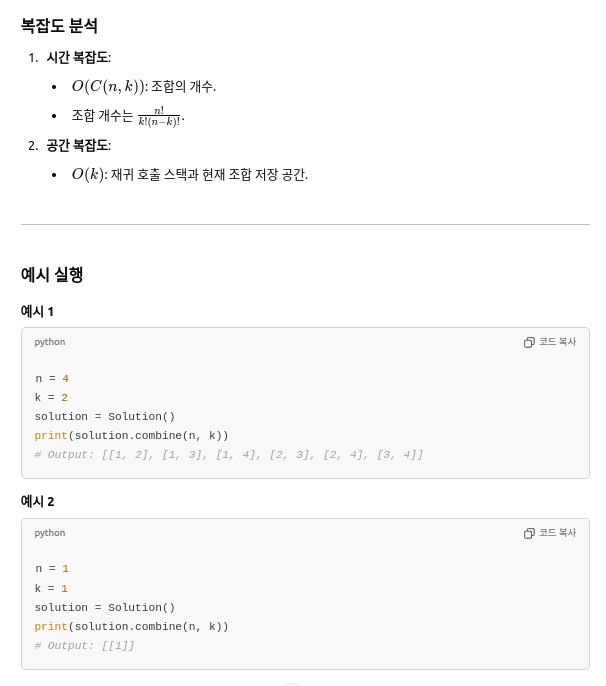
✅ 부분집합이란?Set A가 Set B의 부분집합이라는 것은 → A에 있는 모든 원소가 B에도 있어야 함.기호로는 A ⊆ B 로 씀.📌 중요한 성질모든 집합은 자기 자신의 부분집합이다.예: A ⊆ A**공집합(∅)**은 모든 집합의 부분집합이다.예: ∅ ⊆ A (어떤 A라도)원소의 순서는 중요하지 않음.예: {1,2,3}과 {3,1,2}는 같은 집합.원소는 중복될 수 없음.예: {1,1,2}는 {1,2}와 같은 집합으로 본다.✔ 예시 복습A = {1,2,3,4,5}, B = {5,2,1} → ✅ B는 A의 부분집합B = {2,5,1} → ✅ 여전히 부분집합 (순서 상관 없음)C = {9,10,11,12}, D = {6,9,10} → ❌ D는 C의 부분집합 아님 (6이 C에 없음)✅ 부분집합이란?n개의 ..

90. Subsets II https://youtu.be/Vn2v6ajA7U0?si=w1awdAmx7zve9Tqv class Solution: def subsetsWithDup(self, nums: List[int]) -> List[List[int]]: # Sort the input list to group duplicates together # 입력 리스트를 정렬하여 중복된 숫자를 연속적으로 배치 nums.sort() # List to store all unique subsets # 모든 고유한 부분집합을 저장할 리스트 res = [] # Backtracking function # 백트래킹 함수 정..

78. Subsets https://youtu.be/REOH22Xwdkk?si=J1EDs8ppnu7DJndK class Solution: def subsets(self, nums: List[int]) -> List[List[int]]: # subset 만들기 res = [] subset = [] def dfs(idx): if idx >= len(nums): print(idx, subset) res.append(subset.copy()) return # decision to include nums[idx] sub..

39. Combination Sum from typing import Listclass Solution: def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]: res = [] def backtrack(start, comb, total): # Base case: 합이 target과 같으면 결과에 추가 if total == target: res.append(comb.copy()) return # 합이 target을 초과하면 더 이상 탐색하지 않음 if tot..

77. Combinations https://youtu.be/q0s6m7AiM7o?si=im6vNN9SG6FK35Vs 풀이 과정문제 이해:n: 1부터 n까지의 숫자.k: 조합에 포함할 숫자의 개수.조합은 순서가 중요하지 않음.백트래킹 전략:숫자 1부터 n까지 반복하며 k개의 숫자를 선택.선택된 숫자는 조합에 추가.조합이 k개의 숫자를 만족하면 결과에 추가.선택한 숫자를 다시 되돌려가며 새로운 조합을 탐색.최적화:현재 숫자 iii를 선택한 뒤에는 i+1부터 탐색.중복된 조합 생성을 방지.class Solution: def combine(self, n: int, k: int) -> List[List[int]]: res = [] # 결과를 저장할 리스트 # 백트래킹 함수 정의 ..