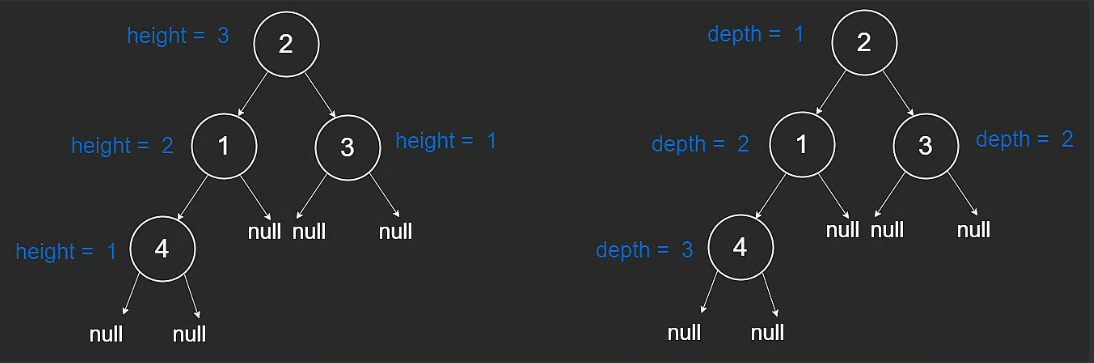
height 는 자식이 없는 노드가 1이고
Depth 는 부모 root 노드가 1로 시작
DFS 검색 방법: 깊이 우선 탐색 (Depth-First Search, DFS)
깊이 우선 탐색(DFS)은 코딩 인터뷰에서 가장 자주 등장하는 알고리즘 중 하나입니다. 주로 트리나 그래프를 탐색할 때 사용됩니다. 이 강의에서는 트리 탐색에 초점을 맞춰 설명하겠습니다.
트리 전체를 탐색하려면 모든 노드를 방문해야 합니다. 이때 사용할 수 있는 방법 중 하나가 깊이 우선 탐색입니다.
기본 아이디어는 어떤 방향(예: 왼쪽) 을 먼저 선택해서, 해당 방향으로 갈 수 있을 때까지 계속 내려가는 것입니다. 즉, 왼쪽 자식 노드를 따라 계속 내려가다가 더 이상 노드가 없으면(null에 도달하면), 부모 노드로 되돌아가서 이번엔 오른쪽 자식으로 이동합니다.
이 과정을 반복하면서 트리의 모든 노드를 방문합니다.
이것이 깊이 우선 탐색의 핵심입니다.
이름 그대로, 가능한 가장 깊은 곳까지 내려갔다가 다시 되돌아오는(backtrack) 방식으로 탐색하는 방법입니다.
DFS에는 크게 세 가지 순회 방식이 있습니다:
- 중위 순회 (Inorder)
- 전위 순회 (Preorder)
- 후위 순회 (Postorder)
깊이 우선 탐색은 보통 재귀 함수를 이용해 구현하는 것이 가장 자연스럽지만, 스택을 사용한 반복문 방식으로도 구현할 수 있습니다.
Depth-First Search
Depth First Search (DFS) is one of the most common algorithms in coding interviews. It is commonly used to traverse trees and graphs. In this lesson we will focus on trees.
If we want to traverse an entire tree, we have to visit every node. One way to accomplish this is by using depth-first search.
The idea is we pick a direction, say left, and keep following pointers as far down left as we can go until we reach null. Once we reach null, we backtrack to the parent node and then go right. We keep doing this until we have visited every node in the tree. This is the essence of depth-first search.
As the name implies, we go as deep as possible before we backtrack.
There are three ways to traverse a tree using depth-first search:
- Inorder
- Preorder
- Postorder
Depth first search is best implemented using recursion, although it is possible to implement it iteratively using a stack.
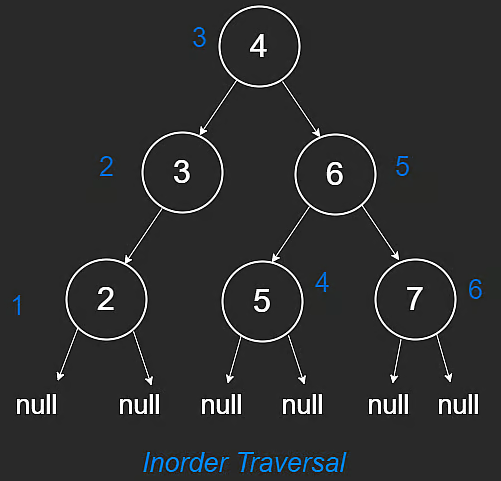
1) inorder traversal: 왼쪽 -> 나 -> 오른쪽
def inorder(root):
if not root:
return
inorder(root.left)
print(root.val)
inorder(root.right)
왼쪽 끝까지 먼저 들어가서, 다시 올라오는 방향으로..
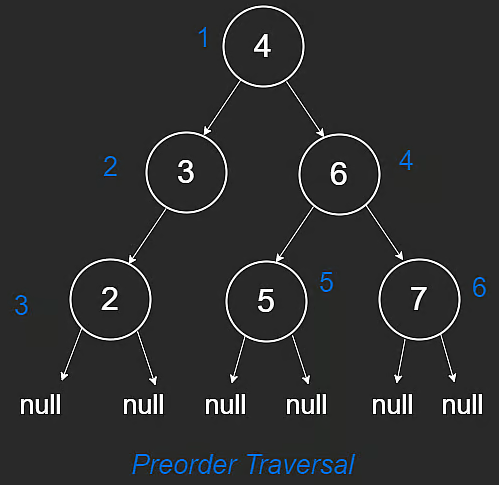
2) preorder traversal: 나 -> 왼쪽 -> 오른쪽
def preorder(root):
if not root:
return
print(root.val)
preorder(root.left)
preorder(root.right)
루트부터.. 그다음 왼쪽.. 오른쪽
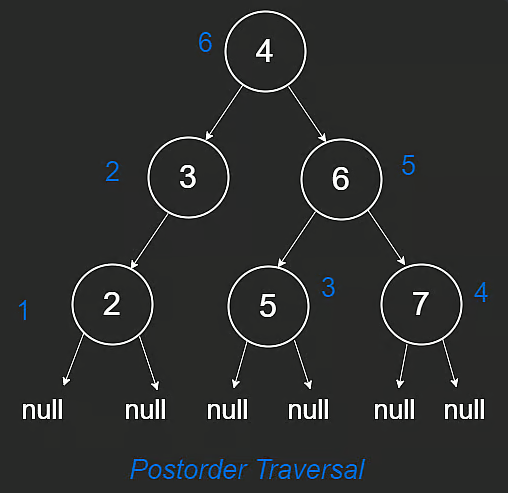
3) postorder traversal: 왼쪽 -> 오른쪽 -> 나
def postorder(root):
if not root:
return
postorder(root.left)
postorder(root.right)
print(root.val)
✅ 1. Inorder Traversal (중위 순회: Left → Root → Right)
🔸 언제 쓰나?
- 이진 탐색 트리(BST) 관련 문제에서 많이 사용돼요.
- 정렬된 결과가 필요할 때 적합해요.
🔸 대표 문제 유형
- BST에서 k번째 작은 값 찾기 (Kth Smallest Element in a BST)
- BST가 올바른지 확인 (Validate Binary Search Tree)
- BST에서 두 노드 스왑된 경우 복원하기 (Recover BST)
- BST → 정렬된 배열로 변환 등
| LeetCode | 94 | Binary Tree Inorder Traversal |
| LeetCode | 230 | Kth Smallest Element in a BST |
| LeetCode | 99 | Recover Binary Search Tree |
| LeetCode | 98 | Validate Binary Search Tree |
| LeetCode | 783 | Minimum Distance Between BST Nodes |
| HackerRank | - | Tree: Inorder Traversal |
🔸 이유
- BST는 왼쪽 < 루트 < 오른쪽 구조니까, inorder로 순회하면 항상 오름차순 정렬된 값이 나와요.
✅ 2. Preorder Traversal (전위 순회: Root → Left → Right)
🔸 언제 쓰나?
- 트리 구조 복원 / 저장할 때 자주 사용돼요.
- 노드를 방문하면서 바로 처리해야 하는 경우 (예: 노드 생성, 누적 계산)
🔸 대표 문제 유형
- 트리를 배열에서 복원 (Construct Binary Tree from Preorder and Inorder)
- 트리를 복사하거나 직렬화 (Serialize and Deserialize Binary Tree)
- 루트에서 리프까지 경로 만들기
- DFS 백트래킹에서 루트 기준 처리 필요할 때
| LeetCode | 144 | Binary Tree Preorder Traversal |
| LeetCode | 1008 | Construct BST from Preorder Traversal |
| LeetCode | 105 | Construct Binary Tree from Preorder and Inorder |
| LeetCode | 129 | Sum Root to Leaf Numbers |
| LeetCode | 297 | Serialize and Deserialize Binary Tree |
| HackerRank | - | Tree: Preorder Traversal |
🔸 이유
- 루트부터 먼저 처리하므로, 트리의 구조를 만들거나, 루트 기반 작업이 용이해요.
✅ 3. Postorder Traversal (후위 순회: Left → Right → Root)
🔸 언제 쓰나?
- 하위 노드부터 계산해서 루트로 올라와야 할 때 사용해요.
- 자식 노드 다 처리한 뒤에 부모를 처리하는 하향식 계산 구조에 적합.
🔸 대표 문제 유형
- 서브트리 합 구하기 (Sum of Subtree)
- 트리 삭제 문제 (Delete Tree, Remove Leaf Nodes)
- 하위 노드 기반 동적 프로그래밍
- 하위 노드 상태를 비교하거나 병합해야 하는 경우 (예: Lowest Common Ancestor)
| LeetCode | 145 | Binary Tree Postorder Traversal |
| LeetCode | 104 | Maximum Depth of Binary Tree |
| LeetCode | 543 | Diameter of Binary Tree |
| LeetCode | 337 | House Robber III |
| LeetCode | 236 | Lowest Common Ancestor of a Binary Tree |
| LeetCode | 863 | All Nodes Distance K in Binary Tree |
| HackerRank | - | Tree: Postorder Traversal |
🔸 이유
- 하위 구조를 먼저 본 다음 루트를 처리하니까, 재귀적으로 계산 누적이 필요할 때 유리해요.
🧠 정리: 문제 유형별 추천 DFS 방식
| 문제 유형 | 추천 DFS 방식 | 이유 |
| BST에서 정렬된 값 필요 | Inorder | 왼 → 중 → 오 순으로 오름차순 출력 |
| 트리 구조 복원, 트리 직렬화/복사 | Preorder | 루트부터 방문하므로 구조 파악 쉬움 |
| 루트에서 리프까지 경로 찾기 | Preorder | 방문 순서가 중요할 때 |
| 하위 노드부터 계산해야 하는 문제 | Postorder | 자식 처리 후 부모 계산 가능 |
| 트리의 합, 삭제, 병합 | Postorder | 자식부터 결과 계산하고 루트에 적용 |
'Coding Test > 알고리즘 이론' 카테고리의 다른 글
| Kadane's Algorithm 카데인 알고리즘: 부분 배열의 최대 합 (0) | 2025.04.04 |
|---|---|
| BST 이진 검색 트리(BFS 너비 우선 탐색, 가까운 노드부터, 큐 사용) (0) | 2025.03.31 |
| DP: 0 / 1 Knapsack 이론 (0) | 2025.02.05 |
| Sorting: Bucket Sort (0) | 2025.02.04 |
| BIT 연산 Bit Manipulation (0) | 2025.01.30 |