**카데인 알고리즘(Kadane's Algorithm)**은 이런 상황에서 사용돼요:
✅ 언제 사용하는가?
**"연속된 부분 배열(subarray) 중에서 가장 큰 합을 구하는 문제"**가 나오면 무조건 카데인 알고리즘을 생각하세요.
✅ 예시 문제 유형:
- 정수 배열이 주어졌을 때, 부분 배열의 최대 합을 구하라.
- 예: [-2, 1, -3, 4, -1, 2, 1, -5, 4] → 답: 6 ([4, -1, 2, 1])
- 일부 변형으로는 다음도 포함돼요:
- 연속된 일 수 동안의 최대 이익
- 연속된 구간에서 최대 에너지, 기쁨, 포인트 등등…
- 부호가 섞인 값에서 연속 부분 최대화 문제
✅ 왜 좋은가?
- 시간 복잡도 O(n) → 매우 빠름
- 공간 복잡도 **O(1)**도 가능 → 메모리 효율적
✅ 쓰지 말아야 할 때?
- "부분 수열(subsequence)" 문제인 경우 (연속X)에는 쓰면 안 돼요. → 이건 보통 다른 DP 문제로 풉니다.
- 예: 증가하는 부분 수열 (LIS), 연속되지 않은 선택 문제 등
최대 합을 가지는 Non-empty subarray 를 찾는데 있어서
=> Subarray 정의: 연속한 배열임
1) 우선 '브루스 포스'로 풀면 (i, j를 사용하므로 two point 라고 생각해도 됨)
- i = 0 -> j는 0부터 배열끝까지 => 로컬 Sum => global Sum 최대값 갱신
- i=1 -> j는 1부터 배열끝까지 => 로컬 Sum => global Sum 최대값 갱신
- ...
- i=배열끝 -> j는 배열끝 => 로컬 Sum => global Sum 최대값 갱신
- ==> O(n^2)
def bruteForce(nums):
maxSum = nums[0]
for i in range(len(nums)):
curSum = 0
for j in range(i, len(nums)):
curSum += nums[j]
maxSum = max(maxSum, curSum)
return maxSum
2) 누적 Sum 인 curSum 이 마이너스값(negative)이면, 0 으로 세팅되는 로직: curSum = max(curSum, 0)
=> O(n) 연산량!!
def kadanes(nums):
maxSum = nums[0]
curSum = 0
for n in nums:
curSum = max(curSum, 0)
curSum += n
maxSum = max(maxSum, curSum)
return maxSum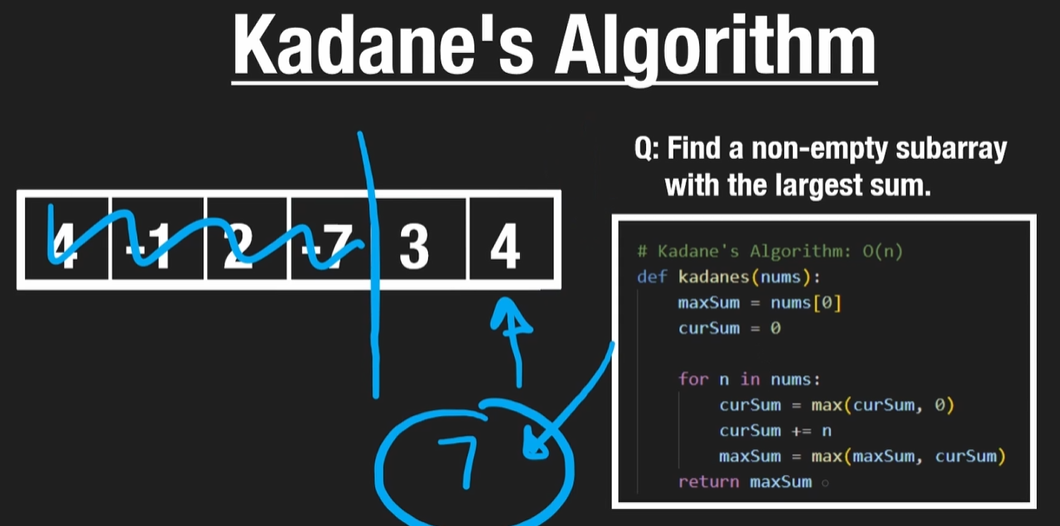
3) two pointer, 슬라이딩 윈도우 활용! ==> 최대합의 인덱스 구할때!!
def slidingWindow(nums):
maxSum = nums[0]
curSum = 0
maxL, maxR = 0, 0
L = 0
for R in range(len(nums)):
if curSum < 0:
curSum = 0
L = R
curSum += nums[R]
if curSum > maxSum:
maxSum = curSum
maxL, maxR = L, R
return [maxL, maxR]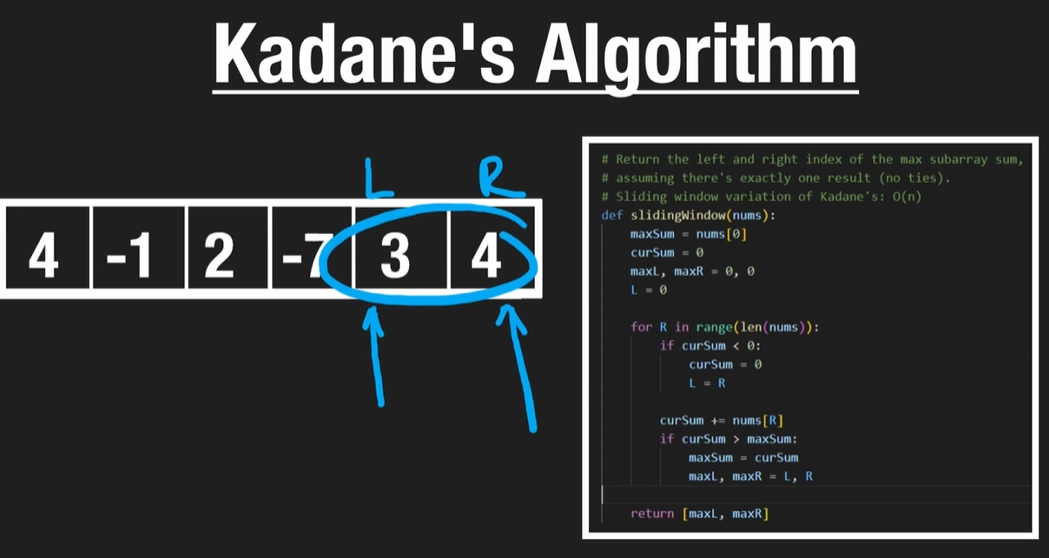
4) DP 로 풀이
✅ 문제:
정수 배열 nums가 주어졌을 때, 연속된 부분 배열(subarray) 중에서 가장 큰 합을 구하라.
✅ 핵심 아이디어 (DP 방식):
- dp[i]는 i번째 원소까지 고려했을 때, i를 포함하는 가장 큰 부분합을 의미해요.
- 점화식:→ 현재 원소 nums[i]를 새로운 시작점으로 삼을지, 이전의 부분합에 더할지 결정하는 구조예요.
dp[i] = max(nums[i], dp[i-1] + nums[i])✅ Python 코드:
def maxSubArray(nums):
n = len(nums)
dp = [0] * n
dp[0] = nums[0]
max_sum = dp[0]
for i in range(1, n):
dp[i] = max(nums[i], dp[i - 1] + nums[i])
max_sum = max(max_sum, dp[i])
return max_sum
✅ 공간 최적화:
위 DP는 dp 배열을 쓰지만, 사실 dp[i]만 알면 dp[i+1] 계산 가능하니까 변수 하나로도 충분해요.
def maxSubArray(nums):
current_sum = max_sum = nums[0]
for i in range(1, len(nums)):
current_sum = max(nums[i], current_sum + nums[i])
max_sum = max(max_sum, current_sum)
return max_sum
'Coding Test > 알고리즘 이론' 카테고리의 다른 글
| Trees: Trie (트라이) (0) | 2025.04.07 |
|---|---|
| Prefix Sum 누적합 (영상처리에서 누적영상) (0) | 2025.04.05 |
| BST 이진 검색 트리(BFS 너비 우선 탐색, 가까운 노드부터, 큐 사용) (0) | 2025.03.31 |
| BST 이진 검색 트리(height, Depth, DFS 검색 방법: inorder, preorder, postorder) (0) | 2025.03.31 |
| DP: 0 / 1 Knapsack 이론 (0) | 2025.02.05 |